ランダウ・リフシッツ力学 §32 問題1 ｃ

ランダウ・リフシッツの力学(増補第3版) §32 問題1 c のメモです。

正三角錐は底面が正三角形の錐体のことです。

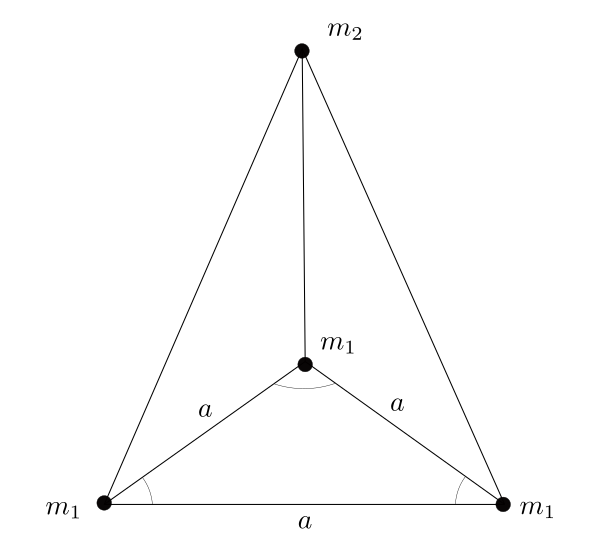
慣性中心を計算します。原点を底面の重心にします。

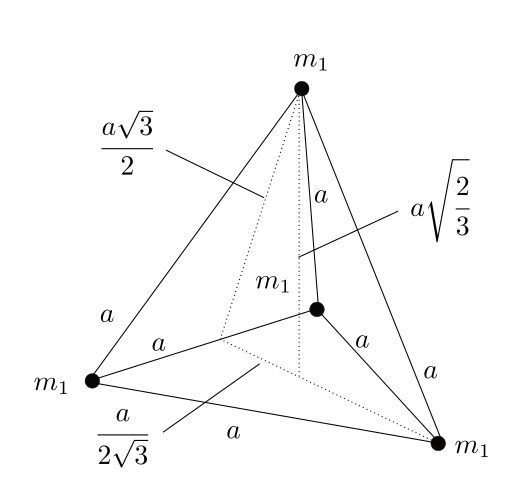
\[ \boldsymbol{R} = \cfrac{1}{\mu} \sum m\boldsymbol{r}= (0,0, \cfrac{1}{\mu} m_2 h) \]

底面の各頂点の位置関係は下の図のようになります:

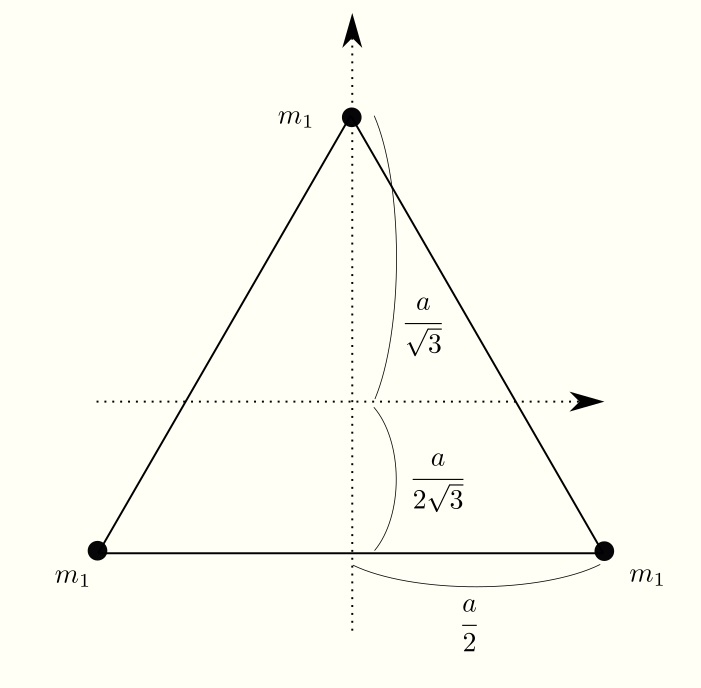\begin{align} I_1 & = \sum m(y^2 + z^2) \\ & = m_1 \left[2\times \left(\cfrac{a}{2\sqrt{3}}\right)^2 + \left(\cfrac{a}{\sqrt{3}}\right)^2 \right] + 3\times m_1 \left(\cfrac{m_2 h}{\mu}\right)^2 + m_2 \left(h – \cfrac{m_2 h}{\mu} \right)^2 \\ & = m_1 \cfrac{a^2}{2} + \cfrac{h^2 m_2}{\mu^2} \left[3m_1m_2 + \left(3m_1 \right)^2 \right]\\ & = \cfrac{m_1 a^2}{2} + \cfrac{h^2 m_2}{\mu^2}3m_1 \left( m_2 + 3m_1 \right)\\ & = \cfrac{m_1 a^2}{2} + \cfrac{3m_1 m_2 h^2 }{\mu}\\ & = I_2. \end{align} \begin{align} I_3 &= \sum m (x^2 + y^2) \\ &= m_1 \left[ \left(\cfrac{a}{\sqrt{3}} \right)^2 + 2 \times \left( \cfrac{a}{2} \right)^2 + 2\times \left(\cfrac{a}{2\sqrt{3}}\right)^2 \right] \\ &= m_1 a^2 \left(\cfrac{1}{3} + \cfrac{1}{2} + \cfrac{1}{6} \right) \\ &= m_1 a^2 . \end{align}

\(m_1 = m_2\), \(h = a \sqrt{2/3}\)の場合は慣性モーメントは

\begin{align} I_1 & = \cfrac{3 m_1^2}{4m_1} \cfrac{2}{3}a^2 + \cfrac{m_1}{2} a^2 \\ & = \cfrac{ m_1}{2} a^2 + \cfrac{m_1}{2} a^2 \\ & = m_1 a^2\\ & = I_2 . \end{align}

\(I_3\)は上で計算済みです。