ランダウ・リフシッツの力学(増補第3版) §34 剛体の角運動量 のメモです。
このセクションの話題は剛体の運動方程式についてです。
剛体の自由度についての議論は§31にあります。自由度についておさらいすると、静止座標系に対する運動座標系の配置を与える座標を考えます。その座標とは
- 運動座標系\(\boldsymbol{O}\)の位置\(\boldsymbol{R}\)(動径ベクトル: 3成分)
- 運動座標系の軸方向の三つの角度
目次
剛体の運動量の方程式
剛体の運動量の方程式は、剛体を構成する粒子の運動方程式の和です:
\[ \boldsymbol{P} = \sum \boldsymbol{p} = \sum_i m_i \boldsymbol{V} = \mu \boldsymbol{V}. \]剛体にはたらく力については、各粒子の力の和です:
\[ \boldsymbol{F} = \sum \boldsymbol{f} = \sum \dot{\boldsymbol{p}} = \cfrac{d\boldsymbol{P}}{dt} \]粒子相互にはたらく力はゼロ
この導出の後に書かれているのは粒子間の相互作用についてです。相互にはたらく力(\(\boldsymbol{f}\))が打ち消される ことが結論として述べられています。
これは次のような理屈です:
- 外力がないときは剛体の運動量は保存される。 つまり\(\dot{\boldsymbol{P}=0}\)
- したがって \(\boldsymbol{F}=0\)
- これから\(\sum \boldsymbol{f}=0\)。つまり粒子にはたらく力の和はゼロ。外力がゼロだったから、そのほかの粒子間にはたらく力もゼロ(打ち消し合う)。
外場の中の剛体
外場中の剛体にはたらく力を求めます。
慣性中心\(\boldsymbol{R}_0\)が\(\delta \boldsymbol{R}\)だけ移動すると各粒子の座標\(\boldsymbol{r}_i\)も \(\delta \boldsymbol{R}\)だけ移動することから
\begin{align} \delta U = & \sum_i \cfrac{\partial U}{\partial \boldsymbol{r}_i} \cdot \delta \boldsymbol{r}_i \\ = & \sum_i \cfrac{\partial U}{\partial \boldsymbol{r}_i} \cdot \delta \boldsymbol{R} \\ = & \delta \boldsymbol{R} \cdot \sum_i \cfrac{\partial U}{\partial \boldsymbol{r}_i} \\ = & – \delta \boldsymbol{R} \cdot \sum_i \boldsymbol{f}_i \\ = & – \delta \boldsymbol{R} \cdot \boldsymbol{F} . \\ \end{align}これから
\[ \boldsymbol{F} = -\cfrac{\partial U}{\partial \boldsymbol{R}_0}. \](慣性中心についての微分であることが分かるように添え字のゼロをつけました。)
式 (34.1)をラグランジュ方程式から導出する
ラグランジアン
\[ L = \cfrac{\mu V^2}{2} -U \]のラグランジュ方程式
\[ \cfrac{d}{dt} \cfrac{\partial L}{\partial \boldsymbol{V}} = \cfrac{\partial L}{\partial \boldsymbol{R}} \]から導出してみます。
\[ \cfrac{d}{dt}\cfrac{\partial L}{\partial \boldsymbol{V}} = \cfrac{d}{dt} \cfrac{\partial }{\partial \boldsymbol{V}} \left( \cfrac{\mu V^2}{2} -U \right) = \cfrac{d \mu \boldsymbol{V}}{dt} = \cfrac{d \boldsymbol{P}}{dt} , \]また、
\[ \cfrac{\partial L}{\partial \boldsymbol{R}} =\cfrac{\partial }{\partial \boldsymbol{R}} \left( \cfrac{\mu V^2}{2} -U \right) = -\cfrac{\partial U }{\partial \boldsymbol{R}} = \boldsymbol{F}. \]これから
\[ \cfrac{d \boldsymbol{P}}{dt} = \boldsymbol{F}. \]角運動量の運動方程式
「静止基準系をある瞬間の慣性中心が静止しているように選ぶ」のがミソでしょう。 こうすると\(\boldsymbol{V}=0\), またその瞬間の各粒子の速度は\(\boldsymbol{v} = \dot{\boldsymbol{r}}\)となりま す。 すると\(\dot{\boldsymbol{r}} \times \boldsymbol{p} = \boldsymbol{v} \times m \boldsymbol{v} = 0\)。
\[ \dot{\boldsymbol{M}} = \cfrac{d}{dt} \sum \left( \boldsymbol{r} \times \boldsymbol{p} \right) = \sum \left( \dot{\boldsymbol{r}} \times \boldsymbol{p} + \boldsymbol{r} \times \dot{\boldsymbol{p}} \right) = \sum \left( \boldsymbol{r} \times \dot{\boldsymbol{p}} \right) = \sum \left( \boldsymbol{r} \times {\boldsymbol{f}} \right) \equiv \boldsymbol{K} . \]粒子間にはたらく力のモーメント
合力\(\boldsymbol{F}\)の時と同様に、粒子間の相互にはたらく力のモーメントは打ち消し合います。 合力\(\boldsymbol{F}\)の時の議論を力のモーメント・角運動量の保存に読み替えれば良いです。
力のモーメントと原点の選び方
座標原点を\(\boldsymbol{a}\)だけ移動させたとき、物体の新しい各位置ベクトル\(\boldsymbol{r}^{\prime}\)は \(\boldsymbol{r}=\boldsymbol{r}^\prime + \boldsymbol{a}\)と書くことができます。
\begin{align} \boldsymbol{K} = & \sum \left( \boldsymbol{r} \times \boldsymbol{f}\right) = \sum \left( \boldsymbol{r}^\prime \times \boldsymbol{f}\right) + \sum \left( \boldsymbol{a} \times \boldsymbol{f}\right) \\ = & \boldsymbol{K}^\prime + \boldsymbol{a}\times \boldsymbol{F}. \end{align}この式から物体全体にはたらく合力\(\boldsymbol{F}\)がゼロのときは、力のモーメントは座標原点の選び方によらないことが分かります。
回転座標のラグランジュ方程式
ラグランジアン
\[ L = \cfrac{\mu V^2}{2} +\cfrac{1}{2}I_{ik} \Omega_i\Omega_k-U \]からラグランジュ方程式を確認してみます。
ベクトル\(\boldsymbol{\Omega}\)で微分すると、角運動量の定義(式 33.1)から
\[ \cfrac{\partial L}{\partial \Omega_i} = I_{ik}\Omega_k = M_i \]一方 ポテンシャル・エネルギーの変化は
\begin{align} \delta U = & \sum \cfrac{\partial U}{\partial \boldsymbol{r}} \cdot \delta \boldsymbol{r} = – \sum \boldsymbol{f} \cdot \delta \boldsymbol{r} = – \sum \boldsymbol{f} \cdot \left( \delta \boldsymbol{\varphi} \times \boldsymbol{r} \right) \\ = & – \delta \boldsymbol{\varphi} \cdot \sum \left( \boldsymbol{r} \times \boldsymbol{f} \right) = – \delta \boldsymbol{\varphi} \cdot \boldsymbol{K} \end{align}これから
\[ \boldsymbol{K} = – \cfrac{\partial U}{\partial \boldsymbol{\varphi}} = \cfrac{\partial L}{\partial \boldsymbol{\varphi}} . \]これらの結果をラグランジュ方程式
\[ \cfrac{d }{dt} \cfrac{\partial L}{\partial \Omega_i} = \cfrac{\partial L}{\partial \varphi_i} \]に代入すると
\[ \dot{\boldsymbol{M}} = \boldsymbol{K}. \]これで角運動量の運動方程式が回転座標系のラグランジュ方程式から導出できることが確認できました。
\(\boldsymbol{K} \perp \boldsymbol{F}\)となる場合
\(\boldsymbol{K} \perp \boldsymbol{F}\)となる場合について
この場合にはいつも…\(\boldsymbol{K}\prime\)をゼロとするような…ベクトル\(\boldsymbol{a}\)を見いだすことができ る。
という記述について考えます。
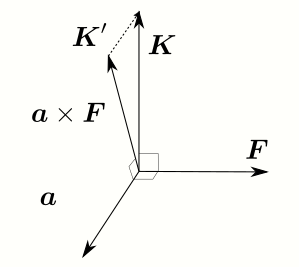
\(\boldsymbol{K} \perp \boldsymbol{F}\)となる場合は下の図のように\(\boldsymbol{a}\)を選ぶと \(\boldsymbol{K}^\prime = 0\)とすることが出来ます。 これは\(\boldsymbol{a}\)と\(\boldsymbol{F}\)を含む平面が\(\boldsymbol{K}\)と垂直になるように\(\boldsymbol{a}\)を選ぶ場合です。
このときは\(\boldsymbol{a}\times\boldsymbol{F}\)の方向が\(\boldsymbol{K}\)と同じになります。

また \(\boldsymbol{a}\)に\(\boldsymbol{F}\)の定数倍を加えても同じ平面(図中の灰色の面)内にありますから、 \(\boldsymbol{a}\times\boldsymbol{F}\)の方向は変わらず\(\boldsymbol{K}\)と同じです。ですから \(\boldsymbol{K}^\prime =0\)とするような\(\boldsymbol{a}\)が一意にきまりません。
では、\(\boldsymbol{a}\)をどのように選ぶと\(\boldsymbol{K}^\prime \not = 0\)になるのでしょうか。
それは\(\boldsymbol{a}\)と\(\boldsymbol{F}\)を含む平面が\(\boldsymbol{K}\)と垂直となっていない場合です(下の図)。 この場合は\(\boldsymbol{a}\times\boldsymbol{F}\)の方向が\(\boldsymbol{K}\)と同じになりません。
ですからゼロでない\(\boldsymbol{K}^\prime\)を含んだ
\[ \boldsymbol{K} = \boldsymbol{K}^\prime + \boldsymbol{a}\times\boldsymbol{F} \]となります。
具体的な例
\[ \boldsymbol{f}=e\boldsymbol{E} \]のような場合
\[ \boldsymbol{F} = \sum \boldsymbol{f} = \sum e \boldsymbol{E}. \]また力のモーメントは
\[ \boldsymbol{K} = \sum \left(\boldsymbol{r} \times \boldsymbol{f} \right)= \sum \left(\boldsymbol{r} \times e \boldsymbol{E}\right). \]これを書き直します:
\[ \boldsymbol{K} = \sum \left(\boldsymbol{r} \times e \boldsymbol{E}\right) = \sum \left( e \boldsymbol{r} \times \cfrac{\boldsymbol{F}}{\sum e} \right) = \cfrac{\sum e \boldsymbol{r}}{\sum e} \times \boldsymbol{F} \equiv \boldsymbol{r}_0 \times \boldsymbol{F}. \]これで\(\boldsymbol{K}=\boldsymbol{a}\times\boldsymbol{F}\)の形になりました (\(\boldsymbol{a}=\boldsymbol{r}_0 \equiv \sum e \boldsymbol{r} /\sum e \))。
これからわかることは、一様な場の中の剛体の運動では場の影響は
\[ r_0 = \cfrac{\sum e \boldsymbol{r}}{\sum e} \]の点での力\(\boldsymbol{F}\)の作用だけ考えれば良いということです。 一様な場の場合は、剛体の運動での影響はある一点だけの影響に代表させることができるということが示されたわけです。
脚注でも書かれていますが具体的な例として以下の二つがあります:
(一様な)重力場の場合
\[ \boldsymbol{F} = m \boldsymbol{g}. \]重力の場合は慣性中心にはたらく重力だけ考えれば良いということです。
(一様な)電場の場合
\[ \boldsymbol{F} = e \boldsymbol{E}. \]電場の場合は「電荷中心」というようなものを考えれば良さそうです。