(更新日: 2019年8月18日 )
ランダウ・リフシッツの力学(増補第3版) §36 問題1 のメモです。
目次
ラグランジアン
\(I_1 = I_2 \not = I_3\)の対称こまを考えます。
ラグランジアンは
\[ L = T_\mathrm{rot} + T_\mathrm{coi} – U \]\(T_\mathrm{coi}\)は慣性中心の運動エネルギーです。coiはCenter of Inertiaの略です。
\(T_\mathrm{rot}\)は式(35.2)から
\[ T_\mathrm{rot} = \cfrac{I_1}{2}\left(\dot{\theta}^2 + \dot{\varphi}^2 \sin^2\theta\right) + \cfrac{I_3}{2}\left(\dot{\varphi} \cos\theta + \dot{\psi}\right)^2. \]\(U\)は慣性中心の高さが原点から\(l \cos\theta\)ですから
\[ U = \mu g l \cos\theta. \]慣性中心の運動を考えます。それには慣性中心の速度を求めます。便宜上、各回転軸での回転による慣性中心の速度を \(V_1, V_2, V_3\)とします。そうすると、まず\(x_3\)軸の回転は慣性中心が動かないので考えなくて良いです。
他方で\(V_1 = l\times \Omega_1\), \(V_2 = l\times \Omega_2\)です。 ですから慣性中心の運動エネルギー\(T_\mathrm{coi}\)は
\begin{align} T_\mathrm{coi} = & \cfrac{\mu }{2} V^2\\ = & \cfrac{\mu }{2} l^2 \left(\Omega_1^2 + \Omega_2^2\right)\\ = & \cfrac{\mu }{2} l^2 \left(\dot{\varphi}^2 \sin^2\theta + \dot{\theta}^2 \right). \end{align}最終的にラグランジアン\(L\)は
\begin{align} L = & \cfrac{I_1}{2}\left(\dot{\theta}^2 + \dot{\varphi}^2 \sin^2\theta\right) + \cfrac{I_3}{2}\left(\varphi \cos\theta + \dot{\psi}\right)^2 \\ & + \cfrac{\mu }{2} l^2 \left(\dot{\varphi}^2 \sin^2\theta + \dot{\theta}^2 \right) – \mu g l \cos\theta \\ = & \left( \cfrac{I_1}{2} +\cfrac{\mu }{2} l^2 \right) \left(\dot{\theta}^2 + \dot{\varphi}^2 \sin^2\theta\right) + \cfrac{I_3}{2}\left(\dot{\varphi} \cos\theta + \dot{\psi}\right)^2- \mu g l \cos\theta. \end{align}「循環的な座標」「運動の積分」のおさらい
「循環的な座標」というのは、ラグランジアンに陽に含まれていない一般座標のこと(本文§14を参照のこと)。
この循環的な座標に対応する一般運動量は運動の積分です。 (「運動の積分」とは運動のあいだ一定の値を保つ量。この量は運動のはじめの条件だけできまります: §6を参照のこと。)
例えば\(q_i\)が循環的であれば
\[ \cfrac{\partial L}{\partial q_i} = 0 \]です。ところでラグランジュ方程式から
\[ \cfrac{\partial L}{\partial q_i} = \cfrac{d}{dt} \cfrac{\partial L}{\partial \dot{q}_i } = \cfrac{d p_i}{dt} =0. \]つまり、\(p_i\)は時間によらず一定の値を保つ量、すなわち運動の積分となります。
運動の積分
今の場合、座標\(\varphi\)と\(\psi\)が陽に含まれていませんから\(p_\varphi\)と\(p_\psi\)の二つの運動の積分があることになります:
\begin{align} p_\psi = & \cfrac{\partial L}{\partial \dot{\psi}} = I_3 \left(\dot{\varphi} \cos\theta + \dot{\psi} \right) = \mathrm{const.} = M_3, \\ p_\varphi = &\cfrac{\partial L}{\partial \dot{\varphi}} = \left( I_1 +\mu l^2 \right) \dot{\varphi} \sin^2\theta + I_3 \cos \theta \left(\dot{\varphi} \cos\theta + \dot{\psi}\right) \\ =& I_1^\prime \dot{\varphi} \sin^2\theta + I_3 \left(\dot{\varphi} \cos^2 \theta + \dot{\psi} \cos \theta \right) \\ =& \left( I_1^\prime \sin^2\theta + I_3 \cos^2\theta \right) \dot{\varphi} + I_3 \dot{\psi} \cos \theta \\ =& \mathrm{const.} = M_z. \end{align}ここで
\[ I_1^\prime \equiv I_1 + \mu l^2. \]エネルギーの表式はラグランジアンのポテンシャル・エネルギーの符号を変えます:
\begin{align} E = & \left( \cfrac{I_1}{2} +\cfrac{\mu }{2} l^2 \right) \left(\dot{\theta}^2 + \dot{\varphi}^2 \sin^2\theta\right) + \cfrac{I_3}{2}\left(\dot{\varphi} \cos\theta + \dot{\psi}\right)^2 + \mu g l \cos\theta \\ = & \cfrac{I_1^\prime}{2} \left(\dot{\theta}^2 + \dot{\varphi}^2 \sin^2\theta\right) + \cfrac{I_3}{2}\left(\dot{\varphi} \cos\theta + \dot{\psi}\right)^2 + \mu g l \cos\theta. \end{align}\(\dot{\psi}\)と\(\dot{\varphi}\)を解きます:
まず
\[ \dot{\psi} = \cfrac{M_3}{I_3} – \dot{\varphi} \cos\theta. \]これを\(\dot{\varphi}\)の表式に代入します:
\begin{align} \left( I_1^\prime \sin^2\theta + I_3 \cos^2\theta \right) \dot{\varphi} + I_3 \left( \cfrac{M_3}{I_3} – \dot{\varphi} \cos\theta \right) \cos \theta = & M_z \\ \left( I_1^\prime \sin^2\theta + I_3 \cos^2\theta \right) \dot{\varphi} + M_3 \cos \theta – \dot{\varphi} I_3 \cos^2\theta = & M_z \\ I_1^\prime \dot{\varphi} \sin^2\theta = & M_z – M_3 \cos\theta\\ \dot{\varphi} = & \cfrac{M_z – M_3 \cos\theta}{I_1^\prime \sin^2\theta} . \end{align}これを\(\dot{\varphi}\)の表式に入れます:
\[ \dot{\psi} = \cfrac{M_3}{I_3} – \cos\theta \cfrac{M_z – M_3 \cos\theta}{I_1^\prime \sin^2\theta} . \]エネルギーの式にこれら\(\dot{\psi}\)と\(\dot{\varphi}\)を代入します:
\begin{align} \dot{\varphi} \cos\theta + \dot{\psi} = & \cos\theta \cfrac{M_z – M_3 \cos\theta}{I_1^\prime \sin^2\theta} + \cfrac{M_3}{I_3} – \cos\theta \cfrac{M_z – M_3 \cos\theta}{I_1^\prime \sin^2\theta} \\ = & \cfrac{M_3}{I_3}. \\ \end{align} \begin{align} E = & \cfrac{I_1^\prime}{2} \left(\dot{\theta}^2 + \dot{\varphi}^2 \sin^2\theta\right) + \cfrac{I_3}{2}\left(\dot{\varphi} \cos\theta + \dot{\psi}\right)^2 + \mu g l \cos\theta \\ = & \cfrac{I_1^\prime}{2} \left( \dot{\theta}^2 + \sin^2\theta \cfrac{\left( M_z – M_3 \cos\theta \right)^2}{I_1^{\prime 2} \sin^4\theta} \right) + \cfrac{I_3}{2}\cfrac{M_3^2}{I_3^2} + \mu g l \cos\theta \\ = & \cfrac{I_1^\prime}{2} \dot{\theta}^2 + \cfrac{\left( M_z – M_3 \cos\theta \right)^2}{2 I_1^{\prime } \sin^2\theta} + \cfrac{M_3^2}{2 I_3} + \mu g l \cos\theta \\ = & \cfrac{I_1^\prime}{2} \dot{\theta}^2 + \cfrac{M_3^2}{2 I_3} + \mu g l + \cfrac{\left( M_z – M_3 \cos\theta \right)^2}{2 I_1^{\prime } \sin^2\theta} – \mu g l + \mu g l \cos \theta \\ = & \cfrac{I_1^\prime}{2} \dot{\theta}^2 + \cfrac{M_3^2}{2 I_3} + \mu g l + \cfrac{\left( M_z – M_3 \cos\theta \right)^2}{2 I_1^{\prime } \sin^2\theta} – \mu g l (1 – \cos \theta) \\ \end{align} \begin{align} E – \cfrac{M_3^2}{2 I_3} – \mu g l = & \cfrac{I_1^\prime}{2} \dot{\theta}^2 + \cfrac{\left( M_z – M_3 \cos\theta \right)^2}{2 I_1^{\prime } \sin^2\theta} – \mu g l (1 – \cos \theta) \\ \end{align}ここで
\begin{align} E^\prime \equiv & E – \cfrac{M_3^2}{2 I_3} – \mu g l \\ U_\mathrm{eff} \equiv & \cfrac{\left( M_z – M_3 \cos\theta \right)^2}{2 I_1^{\prime } \sin^2\theta} – \mu g l (1 – \cos \theta) \end{align}として
\[ E^\prime = \cfrac{I_1^\prime}{2} \dot{\theta}^2 + U_\mathrm{eff} \]これから積分を作ります。
\begin{align} \left(\cfrac{d\dot{\theta}}{dt}\right)^2 = & \cfrac{2}{I^\prime_1}\left(E^\prime – U_\mathrm{eff}\right) \\ dt = & \cfrac{d\theta}{\sqrt{\cfrac{2}{I^\prime_1}\left(E^\prime – U_\mathrm{eff}\right)} }\\ t = & \int\cfrac{d\theta}{\sqrt{\cfrac{2}{I^\prime_1}\left(E^\prime – U_\mathrm{eff}\right)} } . \end{align}\(\theta\)がとりうる範囲
この積分が実行できる(解を持つ)条件は根号の中が正であることですから
\[ E^\prime \ge U_\mathrm{eff}. \]関数\(U_\mathrm{eff}\)の取りうる値を調べてみます。
\[ U_\mathrm{eff} = \cfrac{\left( M_z – M_3 \cos\theta \right)^2}{2 I_1^{\prime } \sin^2\theta} – \mu g l (1 – \cos \theta) \]ですから\(\theta=0\), \(\theta = \pi\)で\(U_\mathrm{eff} \rightarrow +\infty\)。ただし\(M_z \not = M_3\)。 そもそも\(\theta\)が取りうる範囲は\(0 \le \theta \le \pi \)でしたね。
グラフから\(E^\prime\)よりも下側の部分、つまり\(\theta_1 \le \theta \le \theta_2\)の範囲をとり得ます。
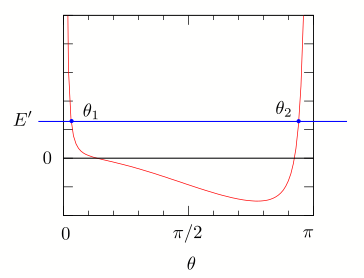
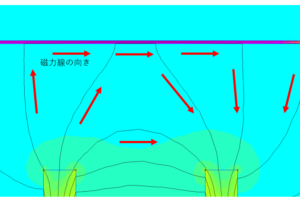
図49の説明(こまの軸の動き)
\[ \dot{\varphi} = \cfrac{M_z – M_3 \cos\theta}{I_1^\prime \sin^2\theta} \]の符号に注目します。
雰囲気を感じるために
このままだと分かりにくいので、雰囲気だけでも味わえるように\(U_\mathrm{eff}\)を簡単に
\[ U_\mathrm{eff} = \left(\theta – \cfrac{\pi}{2}\right)^2 \]のように考えてみます。そうすると
\begin{align} t = & \sqrt{\cfrac{I^\prime}{2}} \int \cfrac{d\theta}{\sqrt{E^\prime -\left(\theta – \cfrac{\pi}{2}\right)^2 }} \\ = & – \sqrt{\cfrac{I^\prime}{2}} \sin^{-1}\cfrac{\pi – 2x}{\sqrt{4 E }} \end{align} \begin{align} \theta = \sqrt{E} \sin \left( \sqrt{\cfrac{2}{I^\prime}} \, \, t \right) + \cfrac{\pi}{2} \end{align}下記グラフでは簡単のため\(I^\prime =2\), \(E^\prime =1\)の場合をプロットしています。
\(\theta\)は\(\theta_1 \le \theta \le \theta_2\)の間で振動しています。
符号が変わらない場合
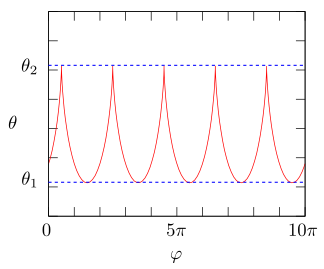
\(\dot{\varphi}\)の符号が変わらないから、\(\varphi\)は単調に増加して行きます。
グラフでは\(\phi = t \)を仮定してプロットしてみました。
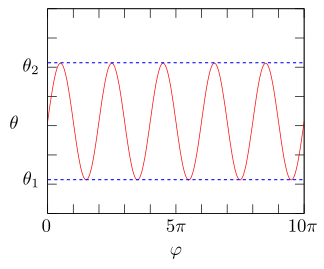
符号が変わる場合
\(\dot{\varphi}\) の符号が変わるため、\(\varphi\)は極値を持ちます。
グラフでは\(\varphi = t + 3 \cos t\)を仮定してみました。
この場合\(\dot{\varphi} = 1 – 3 \sin t\)のように振動しながら符号を変える場合の例です。
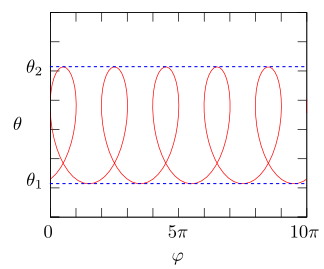
\(\theta_1\), \(\theta_2\)のどちらかで\(\dot{\varphi}\)がゼロになる場合
グラフでは\(\varphi = t + \cos t\)を仮定してみました。
この場合\(\dot{\varphi} = 1 – \sin t\)ですから\(t = \pi/2 + 2n\pi\)(\(n = 0, 1, 2, \cdots\))で\(\dot{\varphi}=0\)になります。
また今の例では\(\dot{\theta} = \sqrt{E} \cos t\)もゼロになります。