(更新日: 2017年8月16日 )
gnuplot の最小二乗フィッティングは他のグラフツールよりも使いやすいと思います。 フィッティングする関数を直接数式で書くことができるので、とても直感的です。
目次
基本形
フィッティング例
下のようなデータをフィッティングする例を考えます。
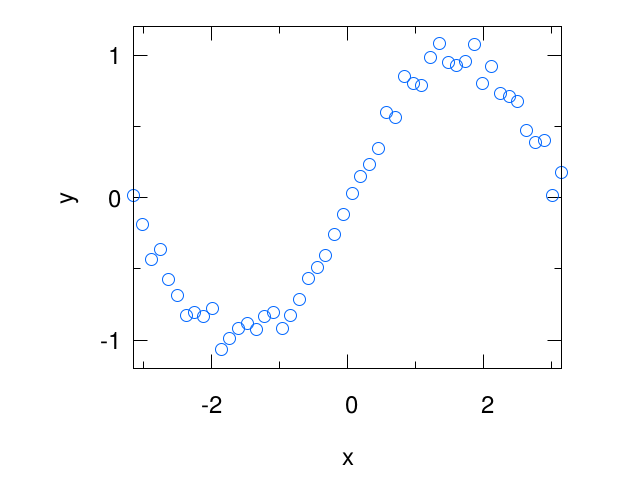
フィッティングするgnuplotのコマンドはfitです。
f(x) = a * x + b a = 2 b = 4 fit [:][:] f(x) 'hoge.dat' using $1:$2 via a,b
のように書きます。
f(x)はフィッティングする関数です。独立変数は12まで、フィッティングするパラメタ数は無制限です!!
フィッティングするパラメタの初期値はa = 2のように指定します。指定しないと、デフォルト値の1からフィッティングを開始します。非線形の最小二乗フィッティングは一般に初期値に依存しますから、初期値を指定するほうが良いでしょう。
fitの後ろの[][]はそれぞれxとyの範囲を指定します。
using はデータのどの列を使うか指定します。
一番最後のvia a,bはフィッティングするパラメタを指定します。
set fit logfile 'hoge.log'
はフィッティング結果を書き込むログファイルを指定します。
下の例では
$$ f(x) = a \sin(bx + x) + d$$
でフィッティングしています。
set terminal pngcairo color enhanced font "Helvetica,18" set output "sin-noise-fit.png" set xlabel 'x' font "Helvetica,18" set ylabel 'y' font "Helvetica,18" set size ratio 0.8 set tics font "Helvetica,18" set xrange [-pi:pi] set yrange [-1.2:1.2] set key left top set xtics 2 set mxtics 2 set ytics 1 set mytics 2 set pointsize 2 set fit logfile "sin-noise-fit.log" f(x) = a * sin(b * x + c) + d fit f(x) 'sin-noise.dat' using ($1):($2) via a,b,c,d plot 'sin-noise.dat' title "data" with points \ lc rgb hsv2rgb(0.6, 1, 1) pt 6,\ f(x) title "fit" with line lt 1 lc rgb hsv2rgb(0, 1, 1) unset output
フィッティング結果
フィッティングした結果を下に示します。
フィッティング後にフィッティング関数をプロットするとフィッティングした結果(フィッティング・パラメタの値)を参照してプロットしてくれます。
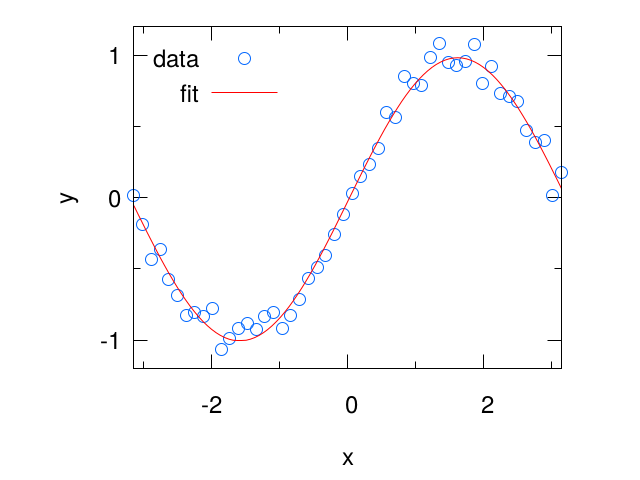
フィッティングする範囲を指定するには(xでもyでも)
xの範囲を[-1:1]に限定するにはfitの後ろに[-1:1]をつけます。
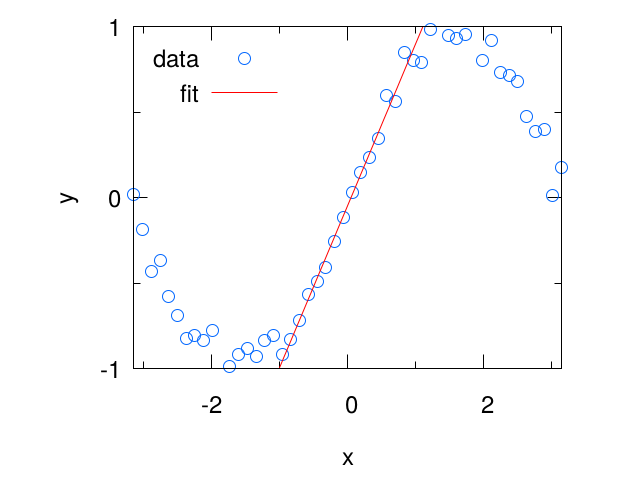
下の例は-1<x<1の範囲で
$$f(x) =ax + b$$
の形でフィッティングしています。
set terminal pngcairo color enhanced font "Helvetica,18" set output "sin-noise-fit-01.png" set xlabel 'x' font "Helvetica,18" set ylabel 'y' font "Helvetica,18" set size ratio 0.8 set tics font "Helvetica,18" set xrange [-pi:pi] set yrange [-1:1] set key left top set xtics 2 set mxtics 2 set ytics 1 set mytics 2 set pointsize 2 set fit logfile "sin-noise-fit-01.log" f(x) = a * x + b fit [-1:1][] f(x) 'sin-noise.dat' using ($1):($2) via a,b plot 'sin-noise.dat' title "data" with points \ lc rgb hsv2rgb(0.6, 1, 1) pt 6,\ f(x) title "fit" with line lt 1 lc rgb hsv2rgb(0, 1, 1) unset output
データがある条件を満足する時だけフィッティングしたい
データがある条件を満足する時だけフィッティングしたい時はusingの部分に条件(三項演算子)をいれることで実現できます。
例えばxデータが正の時だけを使ってフィッティングする場合は
fit f(x) 'hoge.dat' using ($1):($1>0 ? $2 : 1/0)
とします。上の例だとデータ1列目($1)が正の時に2列目($2)をy軸とします。1/0とすると無視されます。
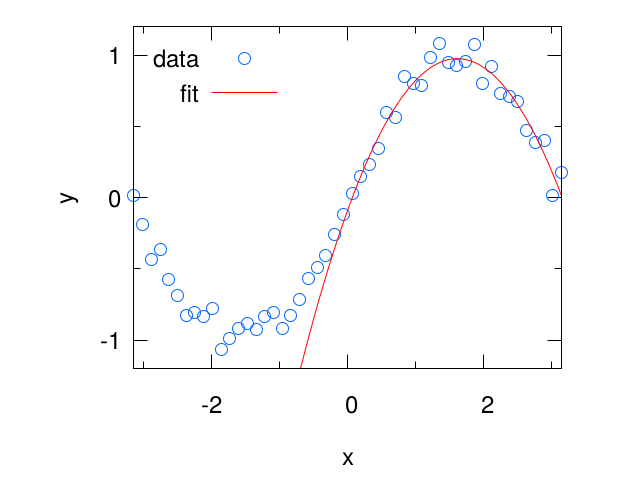
下の例ではxが正の時に
$$ f(x) = a x^2 + b x + c $$
でフィッティングしています。
set terminal pngcairo color enhanced font "Helvetica,18" set output "sin-noise-fit-02.png" set xlabel 'x' font "Helvetica,18" set ylabel 'y' font "Helvetica,18" set size ratio 0.8 set tics font "Helvetica,18" set xrange [-pi:pi] set yrange [-1.2:1.2] set key left top set xtics 2 set mxtics 2 set ytics 1 set mytics 2 set pointsize 2 set fit logfile "sin-noise-fit-02.log" f(x) = a * x ** 2 + b * x + c fit [:][:] f(x) 'sin-noise.dat' using ($1):($1>0? $2 : 1/0) via a,b,c plot 'sin-noise.dat' title "data" with points \ lc rgb hsv2rgb(0.6, 1, 1) pt 6,\ f(x) title "fit" with line lt 1 lc rgb hsv2rgb(0, 1, 1) unset output
制御変数
gnuplot の最小二乗フィッティングは Marquardt-Levenberg 法を使っています。フィッティングを制御する変数がいくつかあります。普通はあまり気にしなくて良いでしょう。
FIT_LIMIT
収束条件を指定します。デフォルト値は1e-05です。一回前と今の二乗残差の比がこの値より小さいと収束と見なされます。
FIT_MAXITER
収束計算の繰り返し回数最大値を指定します。0だと制限なしで繰り返します。
FIT_START_LAMBDA
Marquardt-Levenberg 法で使うラムダ値の開始値を指定します。この値を指定しない場合のデフォルト値は自動計算されます。
FIT_LAMBDA_FACTOR
Marquardt-Levenberg法で使うラムダ値の倍率を指定します。デフォルト値は10.0になっています。
フィッティング・ログの例
フィッティングした際のログの例です。
収束の様子や、フィッティング・パラメタの値が記録されています。
下記の”chisq”は残差を標準偏差で割った値です(http://people.duke.edu/~hpgavin/ce281/lm.pdf):
$$ \chi^2 = \sum_{i=1}^{m}\left[\frac{y-\hat{y}}{\sigma} \right] $$
iter chisq delta/lim lambda a b 0 1.7549801264e+01 0.00e+00 8.21e-01 1.000000e+00 1.000000e+00 1 6.5549231848e-02 -2.67e+07 8.21e-02 9.525350e-01 -3.429805e-03 2 3.6718909495e-02 -7.85e+04 8.21e-03 9.468135e-01 -4.572544e-02 3 3.6718904139e-02 -1.46e-02 8.21e-04 9.468066e-01 -4.574327e-02 iter chisq delta/lim lambda a b After 3 iterations the fit converged. final sum of squares of residuals : 0.0367189 rel. change during last iteration : -1.45873e-07 degrees of freedom (FIT_NDF) : 14 rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 0.0512131 variance of residuals (reduced chisquare) = WSSR/ndf : 0.00262278 Final set of parameters Asymptotic Standard Error ======================= ========================== a = 0.946807 +/- 0.02166 (2.288%) b = -0.0457433 +/- 0.0128 (27.99%) correlation matrix of the fit parameters: a b a 1.000 b -0.000 1.000
“correaltion matrix”って何?
gnuplot のフィッティング結果には、”correaltion matrix”というものが表示されます。対角成分はいつも1です。 非対角要素は、そのフィッティング・パラメタ同士が独立であれば、ゼロに近くなります。
残差ながら、Excelなどで見るピアソンの相関係数とは同じものではないです。