ランダウ・リフシッツの力学(増補第3版) §11 問題2cのメモです。
\[ y = \tan^2 x \]は下のような形です。
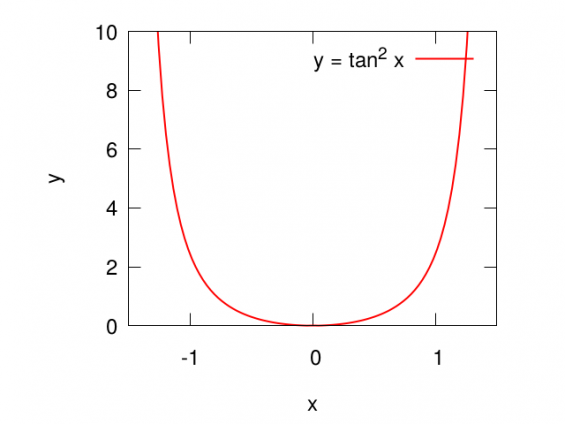
\(x = 0\)について対称ですから、0から停留点\(x_0\)までの積分の2倍です:
\[ T = 2 \sqrt{2m} \int_0^{x_0} \cfrac{dx}{\sqrt{E – U_0 \tan^2 \alpha x}} \]停留点は
\[ \tan^2 \alpha x_0 = \cfrac{E}{U_0} \]の解です。
積分は次のようになります:
\[ T = 2 \sqrt{2m} \int_0^{x_0} \cfrac{\cos \alpha x \, \, dx}{\sqrt{E \cos^2 \alpha x – U_0 \sin^2 \alpha x}} \]変数置換\(u = \sin \alpha x\)と置くと、積分上限は \(u_0 = \sqrt{E/(E+U_0)}\)となります。
積分は以下の通りです:
\begin{align} T = & 2 \sqrt{2m} \int_0^{x_0} \cfrac{ du}{\sqrt{E (1 – u^2) – U_0 u^2 }} \\ = & 2 \sqrt{2m} \int_0^{u_0} \cfrac{ du}{\sqrt{E – (E + U_0) u^2 }} \\ = & 2 \cfrac{\sqrt{2m}}{\sqrt{E + U_0}} \int_0^{u_0} \cfrac{ du}{\sqrt{\cfrac{E}{E + U_0} – u^2 }}\\ = & 2 \cfrac{\sqrt{2m}}{\sqrt{E + U_0}} \left. \sin^{-1}\cfrac{u}{\sqrt{\cfrac{E}{E + U_0} }} \right|_0^{u_0} \\ = & 2 \cfrac{\sqrt{2m}}{\sqrt{E + U_0}} \cfrac{\pi}{2} \\ = & \cfrac{\pi \sqrt{2m}}{\sqrt{E + U_0}} \end{align}L D Landau,E. M. Lifshitz Butterworth-Heinemann 1982-01-29