(更新日: 2019年4月29日 )
ランダウ・リフシッツの力学(増補第3版) §35 オイラーの角 のメモです。 このセクションはオイラーの角の説明です。オイラーの角で表現するとどうなるかを導出します。目次
オイラーの角
オイラーの角とは
オイラーの角について本文中ではほとんど説明がありません。
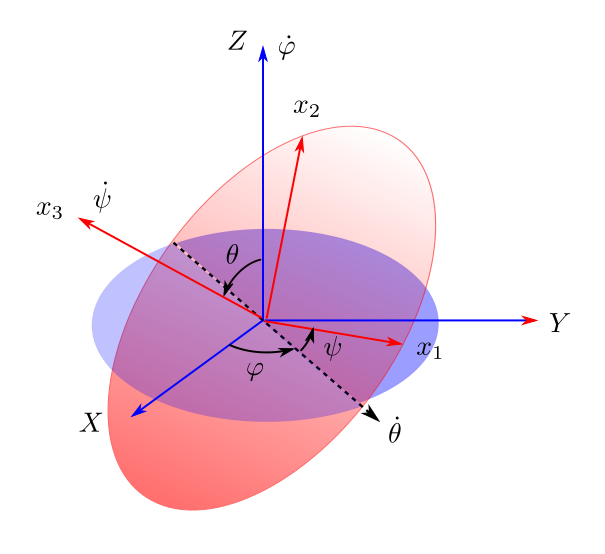
オイラーの角は二つの直交座標系の関係を表現する方法の一つです。二つの座標系は原点\(O\)を同じにします。 オイラーの角は\((\alpha, \beta, \gamma)\) または\(\varphi, \theta, \psi\)を使います。 ランダウ・リフシッツでは\(\varphi, \theta, \psi\)を使っています。
- \(\varphi, \alpha\): \(X\)軸と\(N\)軸の間の角度
- \(\theta, \beta\): \(Z\)軸と\(x_3\)軸の間の角度
- \(\psi, \gamma\): \(N\)軸と \(x_1\)軸の間の角度
角速度\(\dot{\theta}\)
角速度\(\dot{\theta}\)の\(x_1, x_2, x_3\)への投影は図から分かるように
\begin{align} \dot{\theta_1} & = \dot{\theta} \cos \psi \\ \dot{\theta_2} & = – \dot{\theta} \sin \psi \\ \dot{\theta_3} & = 0 . \end{align}角速度\(\dot{\varphi}\)
まず角速度\(\dot{\varphi}\)の\(x_3\)への投影は\(Z\)軸と\(x_3\)軸の間の角度が\(\theta\)ですから\( \dot{\varphi_3} = \dot{\varphi} \cos \theta \)です。
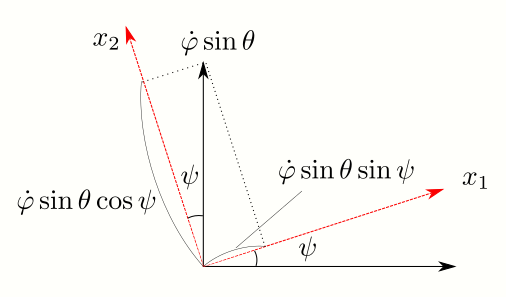
角速度\(\dot{\varphi}\)の\(x_1–x_2\)平面への投影は\( \dot{\varphi} \sin \theta \)です。投影と\(x_2\)との角度が\(\psi\)です。 それを\(x_1\), \(x_2\)に投影するとそれぞれ
\begin{align} \dot{\varphi_1} & = \dot{\varphi} \sin \theta \sin \psi \\ \dot{\varphi_2} & = \dot{\varphi} \sin \theta \cos \psi \\ \dot{\varphi_3} & = \dot{\varphi} \cos \theta . \end{align}角速度\(\dot{\psi}\)
角速度\(\dot{\psi}\)は\(x_3\)の方向を向いているので
\begin{align} \dot{\psi_1} & = \dot{\psi_2} = 0 \\ \dot{\psi_3} & = \dot{\psi}. \end{align}これらから角速度ベクトル\(\boldsymbol{\Omega}\)をオイラーの角で表現すると次のようになります:
\begin{align} \Omega_1 = & \dot{\theta_1} + \dot{\varphi_1} + \dot{\psi_1} = \dot{\varphi} \sin \theta \sin \psi + \dot{\theta} \cos \psi \\ \Omega_2 = & \dot{\theta_2} + \dot{\varphi_2} + \dot{\psi_2} = \dot{\varphi} \sin \theta \cos \psi – \dot{\theta} \sin \psi \\ \Omega_3 = & \dot{\theta_3} + \dot{\varphi_3} + \dot{\psi_3} = \dot{\varphi} \cos \theta + \dot{\psi} . \end{align}運動エネルギーの計算
\(I_1=I_2\not = I_3\)の場合を考えます:
\begin{align} T_\mathrm{rot} & = \cfrac{I_1}{2} \Omega_1^2 + \cfrac{I_2}{2} \Omega_2^2 + \cfrac{I_3}{2} \Omega_3^2 \\ & = \cfrac{I_1}{2} \left[ \left(\dot{\varphi} \sin \theta \sin \psi + \dot{\theta} \cos \psi\right) + \left(\dot{\varphi} \sin \theta \cos \psi – \dot{\theta} \sin \psi \right)\right]^2 + \cfrac{I_3}{2} \left(\dot{\varphi} \cos \theta + \dot{\psi}\right)^2 \\ & = \cfrac{I_1}{2} \left( \dot{\varphi}^2 \sin^2 \theta + \dot{\theta}^2 \right) + \cfrac{I_3}{2} \left(\dot{\varphi} \cos \theta + \dot{\psi}\right)^2. \end{align}別の導出
対称こまの場合は慣性主軸\(x_1, x_2\)を自由に選べます。この場合はONと同じに\(x_1\)を選ぶと\(\psi=0\)。
こうすると
\begin{align} \Omega_1 = & \dot{\theta} \\ \Omega_2 = & \dot{\varphi} \sin \theta \\ \Omega_3 = & \dot{\varphi} \cos \theta + \dot{\psi} \end{align}と簡単になります。これを(32.8)に代入すれば上の式と同じになります。
オイラーの角の応用
この例では\(Z\)軸をこまの保存される角運動量\(\boldsymbol{M}\)の方向にとる場合を挙げています。
\(x_1\)は交線(ON)と一致するとしています。
こうすると上記の結果を用いて
\begin{align} M_1 &= I_1 \Omega_1 = I_1 \dot{\theta} \\ M_2 &= I_1 \Omega_2 = I_1 \dot{\varphi} \sin \theta \\ M_3 &= I_3 \Omega_3 = I_3 \left(\dot{\varphi} \cos \theta + \dot{\psi} \right) . \end{align}一方で\(x_1\)が\(Z\)軸(\(\boldsymbol{M}\))と垂直なので
\begin{align} M_1 & = 0\\ M_2 & = M \sin\theta \\ M_3 & = M \cos \theta. \end{align}これらが等しいと置くと得られるのが次の関係です:
\begin{align} \dot{\theta} & = 0\\ I_1 \dot{\varphi} & = M \\ I_3 (\dot{\varphi} \cos \theta + \dot{\psi}) & = M \cos \theta \end{align}最初の関係から\(\theta = \mathrm{const}\)が得られます。これは\(x_3\)軸と\(Z\)軸の角度が一定を意味しています。
二番目の関係から\(\dot{\varphi} = M/I_1\)。これは§33で得られた歳差運動の角速度です。
最後の関係から\(\Omega_3 = M \cos\theta / I_3\)が得られます。(なんだか当たり前の感じはします…。)
おわりに
「オイラーの角を使うと便利」と本文中にはありますが、この段階ではそれを実感できませんね。
問題を解くと実感できるのでしょうかね。