(更新日: 2019年3月24日 )
ランダウ・リフシッツの力学(増補第3版) §33 剛体の角運動量 のメモです。
このセクションの話題は剛体の角運動量についてです。
つらつらと書かれていますが、話題は大きく分けて二つかなと。
一つは慣性モーメントと角運動量の関係一般式の導出。もう一つは角運動量ベクトルの性質についての考察。
目次
慣性モーメントと角運動量の関係の導出
公式(9.6)は
\[ \boldsymbol{M} = \boldsymbol{M}’+\boldsymbol{R}\times \boldsymbol{P} \]ここで\(\boldsymbol{M}’\)はK’系の角運動量, \(\boldsymbol{R}\)は慣性中心, \(\boldsymbol{P}=\mu \boldsymbol{V}\) です。
座標原点を慣性中心に選ぶと上記で\(\boldsymbol{R}=\boldsymbol{0}\)と置いて\(\boldsymbol{M}=\boldsymbol{M}’\)。 これが「\(\boldsymbol{M}\)が慣性中心に対する運動のみ関する《固有角運動量》\(\boldsymbol{M}’\)と一致する」ということでしょう。
このことから\(\boldsymbol{M}\)の定義中の\(\boldsymbol{v}\)を\(\boldsymbol{\Omega}\times\boldsymbol{r}\)として次のように書きます:
\begin{align} \boldsymbol{M} =& \sum m \boldsymbol{r} \times \boldsymbol{v} \\ = & \sum m \boldsymbol{r} \times \left(\boldsymbol{\Omega} \times \boldsymbol{r} \right) \\ = & \sum m \left(r^2 \boldsymbol{\Omega} – (\boldsymbol{r}\cdot \boldsymbol{\Omega}) \boldsymbol{r} \right). \end{align}テンソル記号を使うと
\begin{align} M_i = & \sum m \left(x_{l}^2 \Omega_i – x_k \Omega_k x_i \right) \\ = & \Omega_k \sum m \left(x_{l}^2 \delta_{ik} – x_i x_k \right) \\ = & I_{ik} \Omega_k \end{align}テンソル表記からも分かりますが、一般的に\(M\)と\(\Omega\)は同じ方向になりませんね。
例えば、一般的な表式では
\[ M_1 = I_{11}\Omega_1 + I_{12}\Omega_2 + I_{13}\Omega_3 \]となって\(M_1\)は\(\Omega_1\)以外の成分にも慣性モーメント系由で依存します。 もしも同じ方向であれば、\(\boldsymbol{M}\)と\(\boldsymbol{\Omega}\)が比例するようになります。
慣性テンソルは対角にすることができて、その時の軸を慣性主軸と呼びます(§32)。この時は定義から対角ですから
\begin{align} M_1 & = I_1 \Omega_1 \\ M_2 & = I_2 \Omega_2 \\ M_3 & = I_3 \Omega_3. \end{align}\(\boldsymbol{M}\)と\(\boldsymbol{\Omega}\)の方向
球状こま
球状こまとは三つの主慣性モーメントが等しい場合のことを言います。この場合\(I_1 = I_2 = I_3\equiv I\)ですから
\[ \boldsymbol{M} = I \boldsymbol{\Omega} \]角運動量ベクトルは角速度ベクトルに比例してと同じ方向を向いています。
孤立した剛体の自由な回転の角運動量は保存されます(角運動量=一定)。 孤立した球状こまの場合\(M=\)一定は\(\Omega=\)一定。
回転子
回転子というのは直線(\(x_3\)軸)に沿って分布した粒子の系(§32)。この場合は
\begin{align} I_1 = & I_2 = I= \sum m x_3^2\\ I_3 = & 0. \end{align}この場合も\(\boldsymbol{M}=I \boldsymbol{\Omega}\)ですが、成分を確かめると
\begin{align} M_1 & = I_1 \Omega_1 \\ M_2 & = I_2 \Omega_2 \\ M_3 & = 0. \end{align}これから\(x_1\)と\(x_2\)成分のみを持ちます。 これから角運動量ベクトル\(\boldsymbol{M}\)は\(x_3\)軸、つまり回転子の軸とは垂直です。
対称こまの複雑な回転
ここで説明しているのは歳差運動している剛体の状況です。 才差運動の角運動量を\(\boldsymbol{M}\), \(x_3\)と角運動量\(\boldsymbol{M}\)との角度が\(\theta\)としています。
\(x_2\)軸を\(\boldsymbol{M}\)と\(x_3\)軸から構成される平面(図中の色のついた平面)と垂直にとります。 こうすると\(\boldsymbol{M}\)の\(x_2\)軸への写影はゼロですから\(M_2=0\)です。 そうすると\(\Omega_2=0\)(\(x_1,x_2, x_3\)を慣性主軸の方向にとっているからです)。
これから\(\boldsymbol{M}, \boldsymbol{\Omega}, x_3\)の三つのベクトルが同一平面内にあることになります。
こまの軸上\(x_3\)の点の速度\(\boldsymbol{v}=\boldsymbol{\Omega} \times \boldsymbol{r}\)はこの平面に垂直。 (ここの言っている意味が分かっていません…。後でもう一度考えてみることにします。)
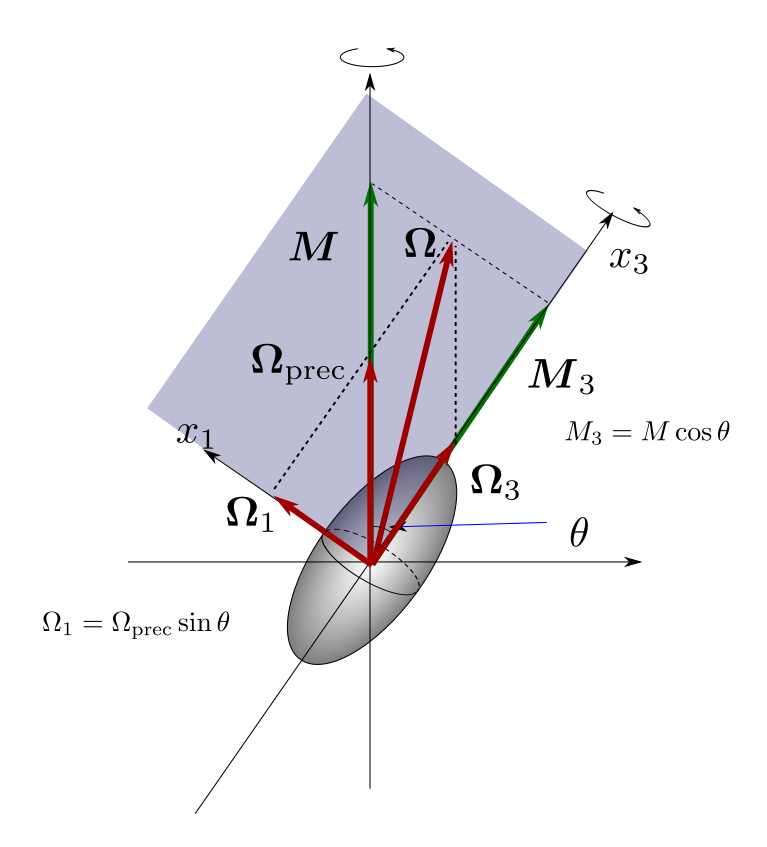
さて剛体全体の角速度\(\boldsymbol{\Omega}\)は才差運動の角速度\(\boldsymbol{\Omega}_\mathrm{prec}\)と\(x_3\)軸上の回転角速度 \(\boldsymbol{\Omega}_3\)の和になります:
\[ \boldsymbol{\Omega} = \boldsymbol{\Omega}_\mathrm{prec} + \boldsymbol{\Omega}_3. \]以下では \(\boldsymbol{\Omega}_3\)と\(\boldsymbol{\Omega}_\mathrm{prec}\)の表式を求めています。
\(M_3 = M \cos \theta\)ですから
\[ \Omega_3 = \cfrac{M_3}{I_3} = \cfrac{M \cos \theta}{I_3}. \]一方才差運動の角速度については\(x_1\)軸上への投影を考えて
\[ \Omega_\mathrm{prec} \sin \theta =\Omega_1 = \cfrac{M_1}{I_1} = \cfrac{M\sin\theta}{I_1} \]これから
\[ \Omega_\mathrm{prec} = \cfrac{M}{I_1}. \]正直言うと、分かったような分からないような感じがしています。 ここのミソは\(\boldsymbol{\Omega_\mathrm{prec}}\sin\theta= \boldsymbol{\Omega_1}\)と出来るのに対して 一方\(\boldsymbol{\Omega_\mathrm{prec}}\cos\theta \not= \boldsymbol{\Omega_3}\)であることかな、と。
本文中の第一の成分とは\(x_3\)軸成分のことで、第二の成分が\(x_1\)軸成分のことでしょう。