(更新日: 2019年3月9日 )
ランダウ・リフシッツの力学(増補第3版) §32 問題7 のメモです。
OAと慣性中心までの距離が\(a \sin \alpha\)ですから、それに角速度を乗じたものが\(Z\)軸の回転の速度と等しいとおきます:
\begin{align} \Omega a \sin \alpha = & V \end{align} \(V =a \dot{\theta} \cos \alpha \) ですから \begin{align} \Omega = & \cfrac{V}{a \sin \alpha} = \cfrac{a \dot{\theta} \cos \alpha}{a \sin \alpha} = \dot{\theta}{\cot \alpha} . \end{align}となります。
慣性主軸は図のように\(x_1\), \(x_3\)をとります。
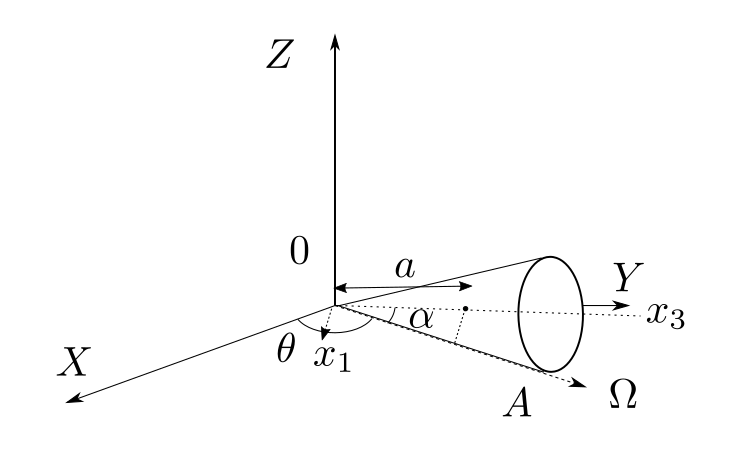
それぞれの軸の角速度ベクトルの写影を\(\Omega_1\), \(\Omega_3\)とすると
\begin{align} \Omega_1 & = \Omega \sin \alpha = \dot{\theta} \cos \alpha \\ \Omega_3 & = \Omega \cos \alpha = \dot{\theta} \cfrac{\cos^2 \alpha}{\sin \alpha}. \end{align}運動エネルギーは
\begin{align} T = & \cfrac{\mu}{2} V^2 + \cfrac{I_1}{2} \Omega_1^2 + \cfrac{I_3}{2} \Omega_3^2 \\ = & \cfrac{\mu}{2} a^2{\dot{\theta}}^2 \cos^2 \alpha + \cfrac{I_1}{2} {\dot{\theta}}^2 \cos^2 \alpha + \cfrac{I_3}{2} {\dot{\theta}}^2 \cfrac{\cos^4 \alpha}{\sin^2 \alpha} . \end{align}ここで問題2-eの結果を使います。
\begin{align} T = & \cfrac{\mu}{2} {\left(\cfrac{3}{4}h\right)}^2{\dot{\theta}}^2 \cos^2 \alpha + \cfrac{1}{2} \cfrac{3}{20}\mu \left(R^2 + \cfrac{h^2}{4} \right) {\dot{\theta}}^2 \cos^2 \alpha + \cfrac{1}{2} \cfrac{3}{10}\mu R^2 {\dot{\theta}}^2 \cfrac{\cos^4 \alpha}{\sin^2 \alpha} \\ = & \cfrac{\mu}{2} {\dot{\theta}}^2 \cos^2 \alpha \left[ \cfrac{9}{16}h^2 + \cfrac{3}{20} \left(R^2 + \cfrac{h^2}{4} \right) + \cfrac{3}{10} R^2 \cot^2\alpha \right] . \end{align}ここで\(\tan \alpha = R/h \)の関係を使って\(R\)と\(a\)を消去します:
\begin{align} T = & \cfrac{\mu}{2} {\dot{\theta}}^2 \cos^2 \alpha \left[ \cfrac{9}{16}h^2 + \cfrac{3}{20} \left(h^2 \tan^2\alpha + \cfrac{h^2}{4} \right) + \cfrac{3}{10} h^2 \tan^2 \alpha \cot^2\alpha \right] \\ = & \cfrac{\mu}{2} {\dot{\theta}}^2 h^2 \cos^2 \alpha \left[ \cfrac{9}{16} + \cfrac{3}{20} \left( \tan^2\alpha + \cfrac{1}{4} \right) + \cfrac{3}{10} \right] \\ = & \cfrac{\mu}{2} {\dot{\theta}}^2 h^2 \cos^2 \alpha \left[ \cfrac{9}{16} + \cfrac{3}{20} \left( \cfrac{1}{\cos^2\alpha} -1 + \cfrac{1}{4} \right) + \cfrac{3}{10} \right] \\ = & \cfrac{\mu}{2} {\dot{\theta}}^2 h^2 \cos^2 \alpha \left[ \cfrac{3}{4} + \cfrac{3}{20} \cfrac{1}{\cos^2\alpha} \right] \\ = & \cfrac{\mu h^2}{2} {\dot{\theta}}^2 \cos^2 \alpha \left[ \cfrac{3}{20} \cfrac{1}{\cos^2\alpha} + \cfrac{15}{20} \right] \\ = & \cfrac{3\mu h^2}{40} {\dot{\theta}}^2 \cos^2 \alpha \left[ \cfrac{1}{\cos^2\alpha} + 5 \right] \\ = & \cfrac{3\mu h^2}{40} {\dot{\theta}}^2 \left[ 1 + 5 \cos^2 \alpha \right] . \end{align}