ランダウ・リフシッツ力学 §32 問題1 b

ランダウ・リフシッツの力学(増補第3版) §32 問題1 b のメモです。

図のように $x_1, x_2$ 軸をとります。

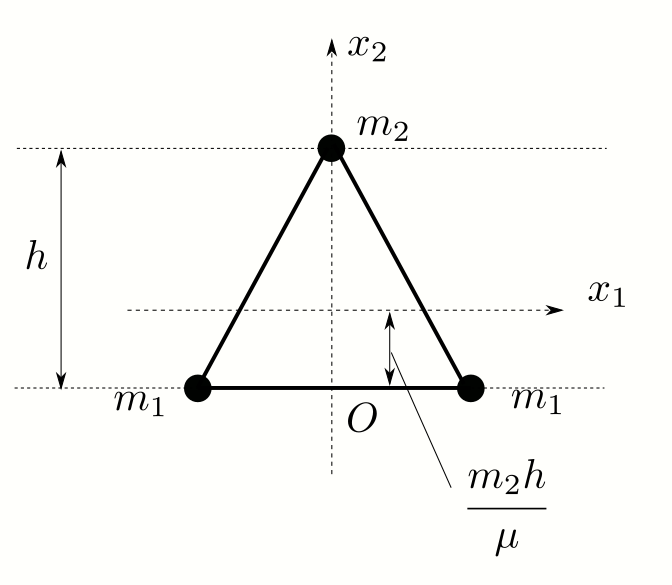
まず慣性中心 $\boldsymbol{R}$ を求めます:

$\boldsymbol{R} = \cfrac{1}{\mu} \sum m \boldsymbol{r}.$

成分で書くと

$\begin{align} X = & 0 \\ Y = & \cfrac{1}{\mu} \sum\left(m_2 h + m_1 \times 0\right) \\ = & \cfrac{1}{\mu} m_2 h \end{align}$

です。

式(32.6)(または式(32.2))から計算します:

$\begin{align} I_1 = I_{11} = & \sum_i m_i y_i^2 \\ = & 2 m_1 \left(-\cfrac{m_2 h}{\mu}\right)^2 + m_2 \left(h – \cfrac{m_2 h}{\mu} \right)^2 \\ = & \cfrac{h^2}{\mu^2} \left[ 2m_1 m_2^2 + m_2 \left(2m_1 + m_2 – m_2 \right)^2 \right] \\ = & \cfrac{h^2}{\mu^2} \left[ 2m_1 m_2^2 + 4 m_1^2 m_2 \right] \\ = & \cfrac{h^2}{\mu^2} 2m_1 m_2 \left( 2 m_1 + m_2 \right) \\ = & \cfrac{h^2}{\mu} 2m_1 m_2 . \end{align}$