ランダウ・リフシッツ力学 §29 問題

ランダウ・リフシッツの力学(増補第3版) §29 問題のメモです。

今回は少し分からない部分があります。

まずは

\[ \gamma \approx 3\omega_0 \] を \[ \gamma = 3\omega_0 + \varepsilon \]

とします。

p112の下段からと同様のことをやります(p112では\(\gamma = 2\omega_0 + \varepsilon\))。

第一近似

式(22.4)で\(\gamma = 3\omega_0+\varepsilon\)を代入すると第一近似は

\begin{align} x^{(1)} =& \cfrac{f}{m(\omega_0^2-9\omega_0^2)} \cos\left(3\omega_0 +\varepsilon \right)t \\ = & -\cfrac{f}{8m \omega_0^2} \cos\left(3\omega_0 +\varepsilon \right)t . \end{align}

第二近似

第二近似はまず式(29.1)

\begin{align} & \ddot{x}^{(1)} + \ddot{x}^{(2)} + 2\lambda \left(x^{(1)} + x^{(2)}\right) + \omega_0^2 \left(x^{(1)} + x^{(2)} \right) \\ = & \cfrac{f}{m}\cos(3\omega_0 + \varepsilon) t – \alpha \left(x^{(1)} + x^{(2)}\right)^2 – \beta \left(x^{(1)} + x^{(2)}\right)^3 \end{align}

を考えます。

第一近似が満たす式

\[ \ddot{x}^{(1)} + 2\lambda x^{(1)} + \omega_0^2 x^{(1)} = \cfrac{f}{m}\cos(3\omega_0 + \varepsilon) t \]

を消すと(第一近似では\(\lambda\)の項は実際には無視して)第二近似の式は

\[ \ddot{x}^{(2)} + 2\lambda x^{(2)} + \omega_0^2 x^{(2)} = – \alpha \left(x^{(1)} + x^{(2)}\right)^2 – \beta \left(x^{(1)} + x^{(2)}\right)^3 \]

となります。

共鳴する項(\(\cos \omega_0 t\)を含む項)だけを残すと

\[ \ddot{x}^{(2)} + 2\lambda x^{(2)} + \omega_0^2 x^{(2)} + \alpha {x^{(2)}}^2 + \beta {x^{(2)}}^3 = – 3\beta x^{(1)} {x^{(2)}}^2 \]

となります。

他の項を確認します。確認する項は\({x^{(1)}}^2, {x^{(1)}}{x^{(2)}}, {x^{(1)}}^2{x^{(2)}}, {x^{(1)}}^3\)です。

\({x^{(1)}}^2\)

まず\({x^{(1)}}^2\)は

\[ {x^{(1)}}^2 \propto \cos^2\left(3\omega_0 + \varepsilon \right)t = \cfrac{1}{2}\left( \cos 2\left(3\omega_0 + \varepsilon \right)t +1 \right) = \cfrac{1}{2}\left[ \cos 6\left(\omega_0 + \cfrac{\varepsilon}{3} \right)t +1 \right] \]

なので全部無視できます。

\({x^{(1)}}{x^{(2)}}\)は、後で分かるように\({x^{(2)}} \propto \cos (\omega_0+\varepsilon/3)t\)なので \(\cos 4 (\omega_0+\varepsilon/3)\) と\(\cos 2(\omega_0+\varepsilon/3)\)の項からなります。ですから無視できます: \[ {x^{(1)}}{x^{(2)}} \propto \cos (3\omega_0+\varepsilon)t \cos \left(\omega_0+\cfrac{\varepsilon}{3} \right)t = \cfrac{1}{2} \left\{ \cos 4\left(\omega_0+\cfrac{\varepsilon}{3}\right)t + \cos 2 \left(\omega_0+\cfrac{\varepsilon}{3} \right)t \right\} \]

\({x^{(1)}}^3\)

次に\({x^{(1)}}^3\)を見てみます。

\begin{align} {x^{(1)}}^3 \propto & \cfrac{1}{2} \left[\cos 6\left(\omega_0 + \cfrac{\varepsilon}{3} \right)t +1\right] \cos 3\left(\omega_0+\cfrac{\varepsilon}{3} \right)t \\ = & \cfrac{1}{2} \left\{\cfrac{1}{2}\left[ \cos 9\left(\omega_0+\cfrac{\varepsilon}{3}\right)t + \cos 3 \left(\omega_0+\cfrac{\varepsilon}{3} \right)t \right] + \cos 3\left(\omega_0+\cfrac{\varepsilon}{3} \right)t \right\} \\ = & \cfrac{1}{4} \cos 9\left(\omega_0+\cfrac{\varepsilon}{3}\right)t + \cfrac{3}{4}\cos 3\left(\omega_0+\cfrac{\varepsilon}{3} \right)t \\ \end{align}

共鳴項(\(\cos \omega_0\)t)は現れませんので、全て無視できます。

\({x^{(1)}}^2{x^{(2)}}\)

最後に\({x^{(1)}}^2{x^{(2)}}\)を調べてみます。

\begin{align} {x^{(1)}}^2{x^{(2)}} \propto & \cfrac{1}{2} \left[\cos 6\left(\omega_0 + \cfrac{\varepsilon}{3} \right)t +1\right] \cos \left(\omega_0+\cfrac{\varepsilon}{3} \right)t \\ = & \cfrac{1}{4} \left[ \cos 7\left(\omega_0+\cfrac{\varepsilon}{3}\right)t + \cos 5 \left(\omega_0+\cfrac{\varepsilon}{3} \right)t \right] + \cfrac{1}{2} \cos \left(\omega_0+\cfrac{\varepsilon}{3} \right)t \end{align}

となります。

つまり\(3\beta {x^{(1)}}^2 x^{(2)}\)も残す必要がありそうです。ですが本文では無視しています。さてどうしたものでしょうか。

これが右辺にあったとすると

\begin{align} -3\beta{x^{(1)}}^2 x^{(2)} & = -3 \beta \cfrac{f^2}{64m^2\omega_0^4} \cfrac{1}{2} \cos\left[ \left(\omega_0+\cfrac{\varepsilon}{3} \right)t +\delta \right] \\ & = – \cfrac{3 \beta f^2}{128 m^2\omega_0^4} \cos\left[ \left(\omega_0+\cfrac{\varepsilon}{3} \right)t +\delta \right] \\ \end{align}

となって\(f^2\)に比例する項になります。下で分かるように\(f\)に比例する項があるので、ここでは無視します。 (この部分はこれで良いのか自信がありません。分かる方はコメント頂けると嬉しいです。)

第二近似の右辺

\({x^{(1)}}{x^{(2)}}^2\)を調べてみます:

\begin{align} {x^{(1)}}{x^{(2)}}^2 \propto & \cos 3\left(\omega_0 + \cfrac{\varepsilon}{3} \right)t \cos^2 \left[\left(\omega_0+\cfrac{\varepsilon}{3} \right)t +\delta \right] \\ =& \cos 3\left(\omega_0 + \cfrac{\varepsilon}{3} \right)t \times \cfrac{1}{2} \left\{ \cos 2\left[\left(\omega_0+\cfrac{\varepsilon}{3} \right)t +\delta \right] + 1 \right\} \\ = & \cfrac{1}{4} \left\{ \cos \left[ 5\left(\omega_0+\cfrac{\varepsilon}{3} \right)t + 2\delta \right] + \cos \left[ \left(\omega_0+\cfrac{\varepsilon}{3} \right)t – 2 \delta \right] \right\} \\ & +\cfrac{1}{2} \cos 3 \left(\omega_0 + \cfrac{\varepsilon}{3} \right)t \\ \end{align}

ここで残すべき項は

\[ \cfrac{1}{4} \cos \left[ \left(\omega_0+\cfrac{\varepsilon}{3} \right)t – 2 \delta \right] \]

となります。

第二近似の式に戻ると、右辺は

\begin{align} – 3\beta x^{(1)} {x^{(2)}}^2 & = -3 b^2\beta \left( – \cfrac{f}{8m\omega_0^2} \right) \cfrac{1}{4} \cos \left[ \left(\omega_0+\cfrac{\varepsilon}{3} \right)t – 2 \delta \right] \\ & = \cfrac{3 b^2\beta f}{32m\omega_0^2} \cos \left[ \left(\omega_0+\cfrac{\varepsilon}{3} \right)t – 2 \delta \right] \\ \end{align}

これを式(29.1)と比較すると

\begin{align} f \rightarrow & \cfrac{3\beta b^2 f}{32\omega_0^2} \\ \varepsilon \rightarrow & \cfrac{\varepsilon}{3} \\ \end{align}

とすると式(29.4)と同様の等式が得られます:

\begin{align} b^2 \left[ \left(\cfrac{\varepsilon}{3} -\kappa b^2\right)^2 +\lambda^2\right] & = \left(\cfrac{3\beta b^2 f}{32\omega_0^2}\right)^2 \cfrac{1}{4m^2 \omega_0^2} \\ & = \cfrac{9\beta b^4 f^2}{2^{10}\omega_0^2} \cfrac{1}{4m^2 \omega_0^2} \\ & = \cfrac{9\beta b^4 f^2}{2^{12} m^2\omega_0^4} \\ & \equiv A b^4 \end{align}

これを\(b\)について解きます。

\begin{align} b^2\left\{Ab^2- \left[ \left(\cfrac{\varepsilon}{3} -\kappa b^2\right)^2 +\lambda^2 + \cfrac{\varepsilon^2}{9}\right] \right\} = &0\\ b^2\left[ \kappa^2 b^4 – \left(\cfrac{2\kappa\varepsilon}{3} + A\right)b^2 + \lambda^2 + \cfrac{\varepsilon^2}{9} \right] = & 0 \end{align} \(b^2\)の解は \begin{align} b & = 0 \\ b^2 & = \cfrac{1}{2\kappa^2} \left[ \left(\cfrac{2\kappa\varepsilon}{3} + A\right) \pm \sqrt{\left(\cfrac{2\kappa\varepsilon}{3} + A\right)^2 -4 \kappa^2\left(\lambda^2 + \cfrac{\varepsilon^2}{9} \right) } \right] \\ & = \cfrac{\varepsilon}{3\kappa} + \cfrac{A}{2\kappa^2} \pm \cfrac{1}{2\kappa^2}\sqrt{ \cfrac{4\kappa\varepsilon A}{3} + A^2 -4 \kappa^2 \lambda^2 } \\ & = \cfrac{\varepsilon}{3\kappa} + \cfrac{A}{2\kappa^2} \pm \cfrac{1}{\kappa}\sqrt{ \cfrac{\varepsilon A}{3\kappa} + \cfrac{A^2}{4\kappa^2} – \lambda^2 }. \end{align}

根号の中が正になるのは

\begin{align} \cfrac{\varepsilon A}{3\kappa} + \cfrac{A^2}{4\kappa^2} – \lambda^2 & \ge 0 \\ \varepsilon & \ge \cfrac{3\kappa}{A }\left( \lambda^2 – \cfrac{A^2}{4\kappa^2} \right) \\ & = \cfrac{3 \left( 4\kappa^2 \lambda^2 – A^2 \right) }{4\kappa A } \equiv \varepsilon_k \end{align}

このときの\(b\)は

\begin{align} b_k^2 & = \cfrac{1}{3\kappa}\cfrac{3 \left( 4\kappa^2 \lambda^2 – A^2 \right) }{4\kappa A } + \cfrac{A}{2\kappa^2} \\ & = \cfrac{ \left( 4\kappa^2 \lambda^2 – A^2 \right) }{4\kappa^2 A } + \cfrac{A}{2\kappa^2} \\ & = \cfrac{ \left( 4\kappa^2 \lambda^2 – A^2 \right) }{4\kappa^2 A } + \cfrac{2A^2}{4\kappa^2A} \\ & = \cfrac{ \left( 4\kappa^2 \lambda^2 + A^2 \right) }{4\kappa^2 A } \end{align}

根号の前の符号の確認

次に根号の前の符号について調べてみましょう。符号が正の場合は\(b^2\)が必ず正になるのは明らかです。

符号が負の場合は

\begin{align} \cfrac{\varepsilon}{3\kappa} + \cfrac{A}{2\kappa^2} \ge \cfrac{1}{\kappa}\sqrt{ \cfrac{\varepsilon A}{3\kappa} + \cfrac{A^2}{4\kappa^2} – \lambda^2 } \end{align}

である必要があります。これが成立するかを調べてみます。両辺を自乗すると

\begin{align} \left(\cfrac{\varepsilon}{3} + \cfrac{A}{2\kappa} \right)^2 & \ge \cfrac{\varepsilon A}{3\kappa} + \cfrac{A^2}{4\kappa^2} – \lambda^2 \\ \cfrac{\varepsilon^2}{9} + \cfrac{A^2}{4\kappa^2} + \cfrac{\varepsilon A}{3\kappa} & \ge \cfrac{\varepsilon A}{3\kappa} + \cfrac{A^2}{4\kappa^2} – \lambda^2 \\ \cfrac{\varepsilon^2}{9} & \ge – \lambda^2 \\ \end{align}

となり、これはいつでも満足しそうです。

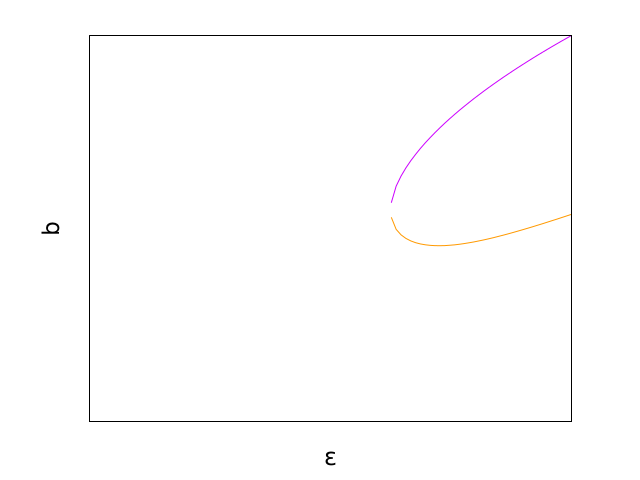
グラフで描いてみると、符号が負の解は符号が正の解と\(b=0\)の間にあるので不安定となります(本文p114に記述があります)。

下のグラフの上側の曲線が根号の前の符号が正のとき、下側が負のときです。

最後の一文

最後の一文は正直よく分かりません。

\(\varepsilon\)が小さいということから\(\varepsilon_k\)も小さいという要求とすると、 \begin{align} \varepsilon_k \sim \cfrac{\kappa \lambda^2}{A} – \cfrac{A}{4\kappa} \ll & \omega_0 \\ \cfrac{\kappa \lambda^2}{A} \ll & \omega_0 + \cfrac{A}{4\kappa}\\ \end{align} ここで \[ \cfrac{A}{\kappa} \ll \omega_0 \] であれば \[ \cfrac{\kappa \lambda^2}{A} \ll \omega_0 \] これから \[ \cfrac{ \lambda^2}{\omega_0} \ll \cfrac{A}{\kappa} \]

となります。これが文意なのかが分かっていません。