ランダウ・リフシッツ力学 §24 問題 2

ランダウ・リフシッツの力学(増補第3版) §24 問題2のメモです。

(今回は長いです。こんなに長くかかるとは思いませんでした(涙目)。)

式(24.1)から \begin{align} m_A(x_1 + x_3) + m_B x_2 & = 0 \\ m_A(y_1 + y_3) + m_B y_2 & = 0 \\ \end{align} 式(24.2)から(\(z\)成分のみを考えると) \begin{align} \sum_{\alpha} \left. m_a \boldsymbol{r}_{0 a} \times \boldsymbol{u}_a \right|_z & = m_A (x_{01}y_1 – y_{01} x_1 ) + m_B (x_{02}y_2 – y_{02} x_2) + m_A (x_{03}y_3 – y_{03} x_3 ) \\ & = m_A ( y_1 \cos(\pi/2 – \alpha) – x_1 \sin(\pi/2 -\alpha) ) + m_A (- y_3 \cos (\pi/2 -\alpha) – x_3 \sin(\pi/2-\alpha) ) \\ & = m_A ( y_1 \sin \alpha – x_1 \cos \alpha ) + m_A (- y_3 \sin \alpha – x_3 \sin \alpha ) \\ & = 0 \end{align} 書き直すと \begin{align} y_1 \sin \alpha – x_1 \cos \alpha – y_3 \sin \alpha – x_3 \sin \alpha & = 0 \\ ( y_1 – y_3 ) \sin \alpha – (x_1 + x_3) \cos \alpha & = 0 . \\ \end{align} 本文では\(\delta l\)としていますが、角度の増分\(\delta\)と紛らわしいので\(\Delta l\)としています。 \(\Delta l\)と\(\delta\)の増分の方向は下図の通りです:

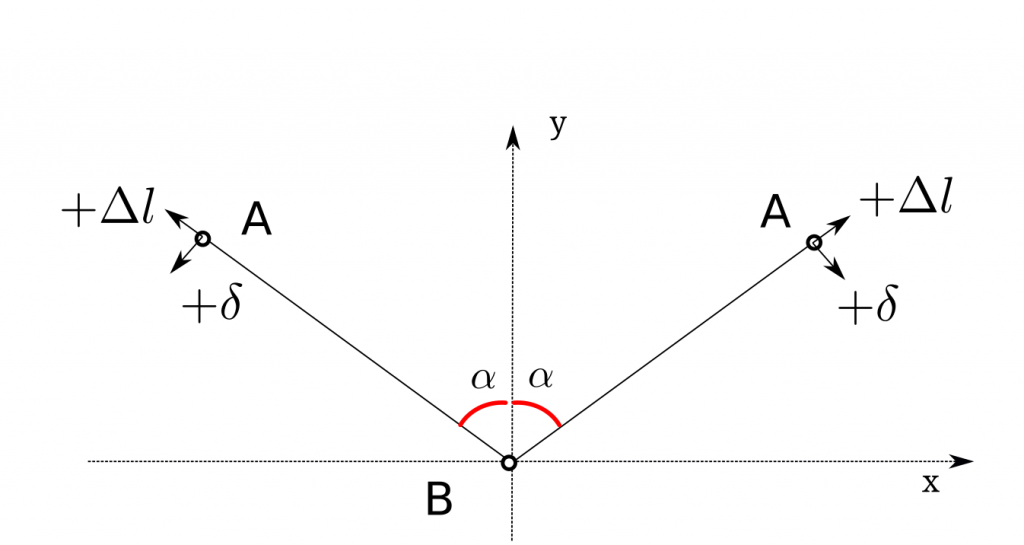矢印の向きが正です。

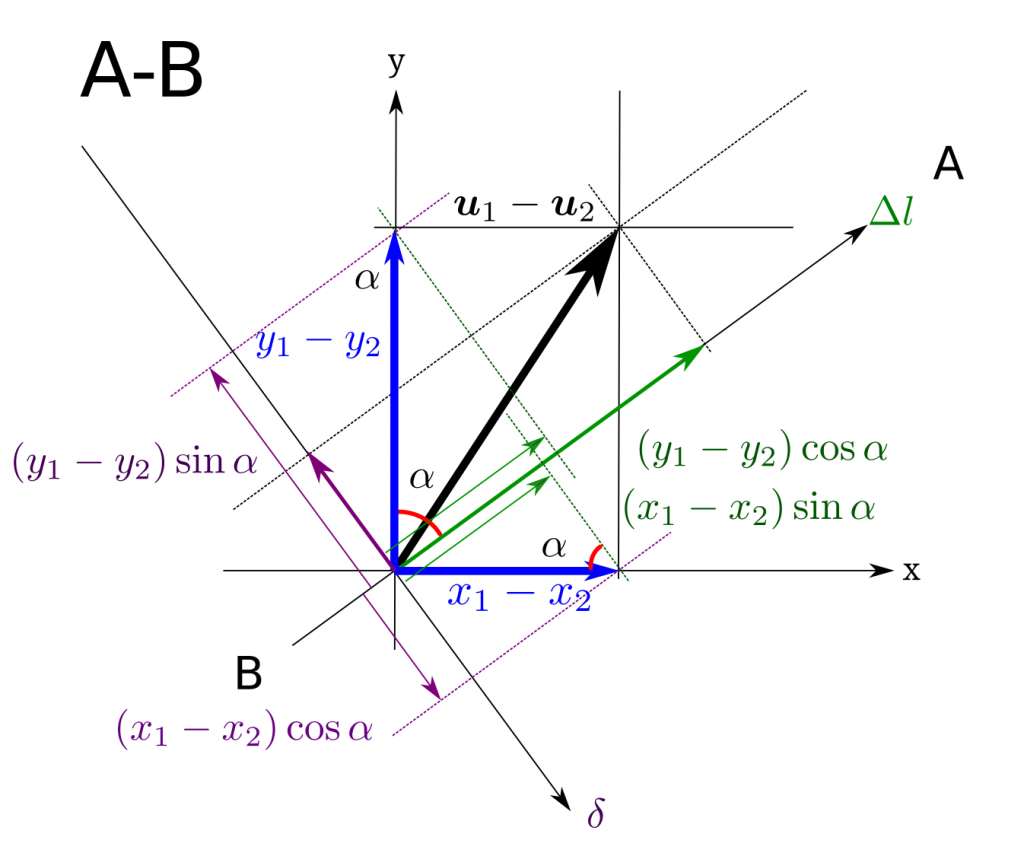質点3 のB-A についての\(\Delta l\)、\(\delta\)の関係は下図の通りです。少し分かりにくいです。

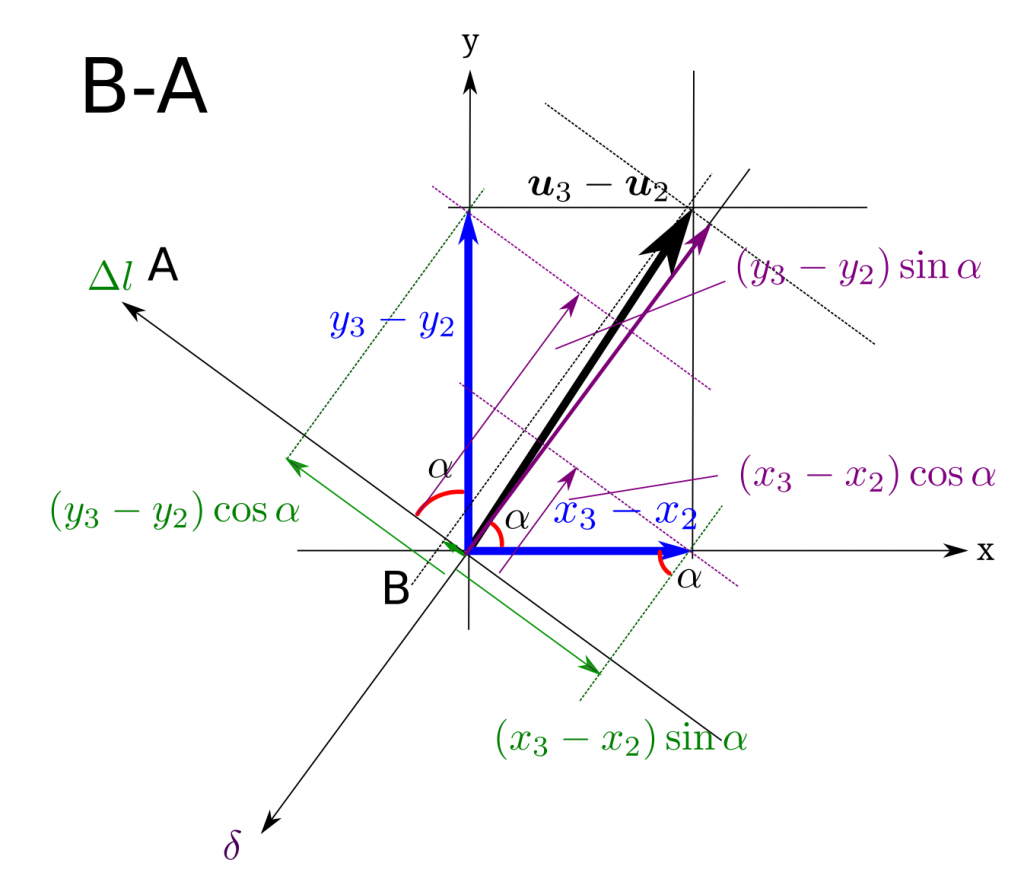\begin{align} x_1 – x_2 =& \cfrac{1}{2} (Q_a + q_{s1}) + \cfrac{m_A}{m_B} Q_a \\ x_3 – x_2 =& \cfrac{1}{2} (Q_a – q_{s1}) + \cfrac{m_A}{m_B} Q_a \\ x_1 – x_3 =& q_{s1} \\ y_1 – y_2 =& \cfrac{1}{2} (q_{s2} + Q_a \cot \alpha) + \cfrac{m_A}{m_B} q_{s2}\\ y_3 – y_2 =& \cfrac{1}{2} (q_{s2} – Q_a \cot \alpha) + \cfrac{m_A}{m_B} q_{s2}\\ y_1 – 2y_2 + y_3 =& q_{s2} + 2\cfrac{m_A}{m_B} q_{s2} = \cfrac{\mu}{m_B} q_{s2}\\ \end{align}

これらを使ってそれぞれ計算していきます。

運動エネルギー

運動エネルギーを計算します:

\begin{align} T_{1,3} = & \cfrac{m_A}{2} (\dot{\boldsymbol{u}}_1^2 + \dot{\boldsymbol{u}}_3^2 ) \\ = & \cfrac{m_A}{2} \left( \cfrac{1}{4}\left( \dot{Q}_a^2 + \dot{q}_{s1}^2 + 2\dot{Q}_a\dot{q}_{s1} \right) + \cfrac{1}{4}\left( \dot{q}_{s2}^2 + \dot{Q}_{a}^2 \cot^2\alpha + 2\dot{Q}_a\dot{q}_{s2} \cot \alpha \right) \right. \\ & \left. + \cfrac{1}{4}\left( \dot{Q}_a^2 + \dot{q}_{s1}^2 – 2\dot{Q}_a\dot{q}_{s1} \right) + \cfrac{1}{4}\left( \dot{q}_{s2}^2 + \dot{Q}_{a}^2 \cot^2\alpha – 2\dot{Q}_a\dot{q}_{s2} \cot \alpha \right) \right) \\ = & \cfrac{m_A}{2} \left( \cfrac{1}{2} ( \dot{Q}_a^2 + \dot{q}_{s1}^2 ) + \cfrac{1}{2} ( \dot{q}_{s2}^2 + \dot{Q}_{a}^2 \cot^2\alpha) \right) \\ = & \cfrac{m_A}{4} \left( \dot{q}_{s1}^2 + \dot{q}_{s2}^2 + \dot{Q}_{a}^2 \cfrac{1}{\sin^2\alpha} \right) \\ \end{align} \begin{align} T_2 = & \cfrac{m_B}{2}\dot{\boldsymbol{u}}_2^2 \\ = & \cfrac{m_B}{2} \left( \cfrac{m_A^2}{m_B^2} (\dot{Q}_a^2 + \dot{q}_{s2}^2) \right) \\ = & \cfrac{m_A^2}{2m_B} (\dot{Q}_a^2 + \dot{q}_{s2}^2) \\ \end{align} \begin{align} T = & T_{1,3} + T_2 \\ = & \cfrac{m_A}{4} \left( \dot{q}_{s1}^2 + \dot{q}_{s2}^2 + \dot{Q}_{a}^2 \cfrac{1}{\sin^2\alpha} \right) + \cfrac{m_A^2}{2m_B} (\dot{Q}_a^2 + \dot{q}_{s2}^2) \\ = & \cfrac{m_A}{4} \dot{q}_{s1}^2 + \left( \cfrac{m_A}{4} + \cfrac{m_A^2}{2m_B} \right) \dot{q}_{s2}^2 + \left( \cfrac{m_A^2}{2m_B} + \cfrac{m_A}{4} \cfrac{1}{\sin^2\alpha} \right) \dot{Q}_{a}^2 \\ = & \cfrac{m_A}{4} \dot{q}_{s1}^2 + \cfrac{m_A}{4}\left( 1 + \cfrac{2m_A}{m_B} \right) \dot{q}_{s2}^2 + \cfrac{m_A}{4} \left( \cfrac{2m_A}{m_B} + \cfrac{1}{\sin^2\alpha} \right) \dot{Q}_{a}^2 \\ = & \cfrac{m_A}{4} \dot{q}_{s1}^2 + \cfrac{m_A \mu }{4} \dot{q}_{s2}^2 + \cfrac{m_A}{4} \left( \cfrac{2m_A}{m_B} + \cfrac{1}{\sin^2\alpha} \right) \dot{Q}_{a}^2 . \end{align}

\(k_2\)のポテンシャル・エネルギー

\(k_2\)のポテンシャル・エネルギーを、ここでは\(U_2\)とします:

\begin{align} U_2 =& \cfrac{k_2}{2} l^2 \delta^2\\ =& \cfrac{k_2}{2} ((x_1 – x_3)\cos \alpha – (y_1 -2y_2 + y_3) \sin \alpha )^2\\ =& \cfrac{k_2}{2} (q_{s1}\cos \alpha – \cfrac{\mu}{m_B} q_{s2} \sin \alpha )^2\\ =& \cfrac{k_2}{2} (q_{s1}^2\cos^2 \alpha + \cfrac{\mu^2}{m_B^2} q_{s2}^2 \sin^2 \alpha – 2 q_{s1}q_{s2} \cfrac{\mu}{m_B} \sin \alpha \cos \alpha )\\ \end{align}

\(k_1\)のポテンシャル・エネルギー

\(k_1\)のポテンシャル・エネルギーを、ここでは\(U_1\)とします:

\begin{align} U_1 =& \cfrac{k_1}{2} (\Delta l_1^2 + \Delta l_2^2)\\ \end{align} \begin{align} \Delta l_1^2 =& \left[ \left(\cfrac{1}{2} (Q_a + q_{s1}) + \cfrac{m_A}{m_B} Q_a \right) \sin \alpha + \left(\cfrac{1}{2} (q_{s2} + Q_a \cot \alpha) + \cfrac{m_A}{m_B} q_{s2} \right) \cos \alpha \right]^2 \\ =& \left(\cfrac{1}{2} (Q_a + q_{s1}) + \cfrac{m_A}{m_B} Q_a \right)^2 \sin^2 \alpha + \left(\cfrac{1}{2} (q_{s2} + Q_a \cot \alpha) + \cfrac{m_A}{m_B} q_{s2} \right)^2 \cos^2 \alpha \\ & + 2\left(\cfrac{1}{2} (Q_a + q_{s1}) + \cfrac{m_A}{m_B} Q_a \right) \left(\cfrac{1}{2} (q_{s2} + Q_a \cot \alpha) + \cfrac{m_A}{m_B} q_{s2} \right)\sin \alpha \cos \alpha. \\ =& \left(\cfrac{1}{2} (Q_a + q_{s1}) + \cfrac{m_A}{m_B} Q_a \right)^2 \sin^2 \alpha + \left(\cfrac{1}{2} (q_{s2} + Q_a \cot \alpha) + \cfrac{m_A}{m_B} q_{s2} \right)^2 \cos^2 \alpha \\ & + 2 \left(\cfrac{1}{4} (Q_a + q_{s1}) (q_{s2} + Q_a \cot \alpha) + \cfrac{1}{2} \cfrac{m_A}{m_B} q_{s2} (Q_a + q_{s1}) + \cfrac{1}{2} \cfrac{m_A}{m_B} Q_a (q_{s2} + Q_a \cot \alpha) + \cfrac{m_A^2}{m_B^2} q_{s2}Q_a \right) \\ & \times \sin \alpha \cos \alpha \\ =& \left(\cfrac{1}{2} (Q_a + q_{s1}) + \cfrac{m_A}{m_B} Q_a \right)^2 \sin^2 \alpha + \left(\cfrac{1}{2} (q_{s2} + Q_a \cot \alpha) + \cfrac{m_A}{m_B} q_{s2} \right)^2 \cos^2 \alpha \\ & + 2 \left(\cfrac{1}{4} (Q_a + q_{s1}) (q_{s2} + Q_a \cot \alpha) + \cfrac{1}{2} \cfrac{m_A}{m_B} q_{s2} Q_a + \cfrac{1}{2} \cfrac{m_A}{m_B} q_{s1} q_{s2} + \cfrac{1}{2} \cfrac{m_A}{m_B} q_{s2} Q_a + \cfrac{1}{2} \cfrac{m_A}{m_B} Q_a^2 \cot \alpha + \cfrac{m_A^2}{m_B^2} q_{s2}Q_a \right) \\ & \times \sin \alpha \cos \alpha \\ =& \left(\cfrac{1}{4} (Q_a + q_{s1})^2 + \cfrac{m_A^2}{m_B^2} Q_a^2 + \cfrac{m_A}{m_B} Q_a (Q_a + q_{s1}) \right) \sin^2 \alpha \\ & + \left(\cfrac{1}{4} (q_{s2} + Q_a \cot \alpha)^2 + \cfrac{m_A^2}{m_B^2} q_{s2}^2 + \cfrac{m_A}{m_B} q_{s2} (q_{s2} + Q_a \cot \alpha) \right) \cos^2 \alpha \\ & + 2 \left(\cfrac{1}{4} ( q_{s1} q_{s2} + q_{s2}Q_a + q_{s1}Q_a\cot \alpha + Q_a^2 \cot \alpha) + \cfrac{1}{2} \cfrac{m_A}{m_B} q_{s2} Q_a + \cfrac{1}{2} \cfrac{m_A}{m_B} q_{s1} q_{s2} + \cfrac{1}{2} \cfrac{m_A}{m_B} q_{s2} Q_a + \cfrac{1}{2} \cfrac{m_A}{m_B} Q_a^2 \cot \alpha + \cfrac{m_A^2}{m_B^2} q_{s2}Q_a \right) \\ & \times \sin \alpha \cos \alpha. \\ \end{align} \begin{align} \Delta l_2^2 =& \left[ -\left(\cfrac{1}{2} (Q_a – q_{s1}) + \cfrac{m_A}{m_B} Q_a \right) \sin \alpha + \left(\cfrac{1}{2} (q_{s2} – Q_a \cot \alpha) + \cfrac{m_A}{m_B} q_{s2} \right) \cos \alpha \right]^2 \\ =& \left(\cfrac{1}{2} (Q_a – q_{s1}) + \cfrac{m_A}{m_B} Q_a \right)^2 \sin^2 \alpha + \left(\cfrac{1}{2} (q_{s2} – Q_a \cot \alpha) + \cfrac{m_A}{m_B} q_{s2} \right)^2 \cos^2 \alpha \\ & – 2\left(\cfrac{1}{2} (Q_a – q_{s1}) + \cfrac{m_A}{m_B} Q_a \right) \left(\cfrac{1}{2} (q_{s2} – Q_a \cot \alpha) + \cfrac{m_A}{m_B} q_{s2} \right)\sin \alpha \cos \alpha. \\ =& \left(\cfrac{1}{2} (Q_a – q_{s1}) + \cfrac{m_A}{m_B} Q_a \right)^2 \sin^2 \alpha + \left(\cfrac{1}{2} (q_{s2} – Q_a \cot \alpha) + \cfrac{m_A}{m_B} q_{s2} \right)^2 \cos^2 \alpha \\ & – 2\left( \cfrac{1}{4} (Q_a – q_{s1})(q_{s2} – Q_a \cot \alpha) + \cfrac{1}{2} \cfrac{m_A}{m_B} q_{s2} (Q_a – q_{s1}) + \cfrac{1}{2} \cfrac{m_A}{m_B} Q_a (q_{s2} – Q_a \cot \alpha) + \cfrac{m_A^2}{m_B^2} q_{s2} Q_a \right) \\ & \times \sin \alpha \cos \alpha \\ =& \left(\cfrac{1}{2} (Q_a – q_{s1}) + \cfrac{m_A}{m_B} Q_a \right)^2 \sin^2 \alpha + \left(\cfrac{1}{2} (q_{s2} – Q_a \cot \alpha) + \cfrac{m_A}{m_B} q_{s2} \right)^2 \cos^2 \alpha \\ & – 2\left( \cfrac{1}{4} (Q_a – q_{s1})(q_{s2} – Q_a \cot \alpha) + \cfrac{1}{2} \cfrac{m_A}{m_B} q_{s2} Q_a – \cfrac{1}{2} \cfrac{m_A}{m_B} q_{s1} q_{s2} + \cfrac{1}{2} \cfrac{m_A}{m_B} q_{s2} Q_a – \cfrac{1}{2} \cfrac{m_A}{m_B} Q_a^2 \cot \alpha + \cfrac{m_A^2}{m_B^2} q_{s2} Q_a \right) \\ & \times \sin \alpha \cos \alpha \\ =& \left(\cfrac{1}{4} (Q_a – q_{s1})^2 + \cfrac{m_A^2}{m_B^2} Q_a^2 + \cfrac{m_A}{m_B} Q_a (Q_a – q_{s1}) \right) \sin^2 \alpha \\ & + \left(\cfrac{1}{4} (q_{s2} – Q_a \cot \alpha)^2 + \cfrac{m_A^2}{m_B^2} q_{s2}^2 + \cfrac{m_A^2}{m_B^2} q_{s2}(q_{s2} – Q_a \cot \alpha)\right) \cos^2 \alpha \\ & – 2\left( \cfrac{1}{4} ( – q_{s1} q_{s2} + q_{s2}Q_a + q_{s1}Q_a \cot\alpha – Q_a^2 \cot \alpha) + \cfrac{1}{2} \cfrac{m_A}{m_B} q_{s2} Q_a – \cfrac{1}{2} \cfrac{m_A}{m_B} q_{s1} q_{s2} + \cfrac{1}{2} \cfrac{m_A}{m_B} q_{s2} Q_a – \cfrac{1}{2} \cfrac{m_A}{m_B} Q_a^2 \cot \alpha + \cfrac{m_A^2}{m_B^2} q_{s2} Q_a \right) \\ & \times \sin \alpha \cos \alpha \end{align} \begin{align} \Delta l_1^2 + \Delta l_2^2 =& \left(\cfrac{1}{4} (Q_a + q_{s1})^2 + \cfrac{m_A^2}{m_B^2} Q_a^2 + \cfrac{m_A}{m_B} Q_a (Q_a + q_{s1}) \right) \sin^2 \alpha \\ & + \left(\cfrac{1}{4} (q_{s2} + Q_a \cot \alpha)^2 + \cfrac{m_A^2}{m_B^2} q_{s2}^2 + \cfrac{m_A}{m_B} q_{s2} (q_{s2} + Q_a \cot \alpha) \right) \cos^2 \alpha \\ & + 2 \left(\cfrac{1}{4} ( q_{s1} q_{s2} + q_{s2}Q_a + q_{s1}Q_a\cot \alpha + Q_a^2 \cot \alpha) + \cfrac{1}{2} \cfrac{m_A}{m_B} q_{s2} Q_a + \cfrac{1}{2} \cfrac{m_A}{m_B} q_{s1} q_{s2} + \cfrac{1}{2} \cfrac{m_A}{m_B} q_{s2} Q_a + \cfrac{1}{2} \cfrac{m_A}{m_B} Q_a^2 \cot \alpha + \cfrac{m_A^2}{m_B^2} q_{s2}Q_a \right) \\ & \times \sin \alpha \cos \alpha \\ & + \left(\cfrac{1}{4} (Q_a – q_{s1})^2 + \cfrac{m_A^2}{m_B^2} Q_a^2 + \cfrac{m_A}{m_B} Q_a (Q_a – q_{s1}) \right) \sin^2 \alpha \\ & + \left(\cfrac{1}{4} (q_{s2} – Q_a \cot \alpha)^2 + \cfrac{m_A^2}{m_B^2} q_{s2}^2 + \cfrac{m_A^2}{m_B^2} q_{s2}(q_{s2} – Q_a \cot \alpha)\right) \cos^2 \alpha \\ & – 2\left( \cfrac{1}{4} ( – q_{s1} q_{s2} + q_{s2}Q_a + q_{s1}Q_a \cot\alpha – Q_a^2 \cot \alpha) + \cfrac{1}{2} \cfrac{m_A}{m_B} q_{s2} Q_a – \cfrac{1}{2} \cfrac{m_A}{m_B} q_{s1} q_{s2} + \cfrac{1}{2} \cfrac{m_A}{m_B} q_{s2} Q_a – \cfrac{1}{2} \cfrac{m_A}{m_B} Q_a^2 \cot \alpha + \cfrac{m_A^2}{m_B^2} q_{s2} Q_a \right) \\ & \times \sin \alpha \cos \alpha \\ =& \left(2\times\cfrac{1}{4} (Q_a^2 + q_{s1}^2 ) + 2\cfrac{m_A^2}{m_B^2} Q_a^2 + 2\cfrac{m_A}{m_B} Q_a^2 \right) \sin^2 \alpha \\ & + \left(2\times\cfrac{1}{4} (q_{s2}^2 + Q_a^2 \cot^2 \alpha) + 2\cfrac{m_A^2}{m_B^2} q_{s2}^2 + 2\cfrac{m_A}{m_B} q_{s2}^2 \right) \cos^2 \alpha \\ & + 4 \left(\cfrac{1}{4} ( q_{s1} q_{s2} + Q_a^2 \cot \alpha) + \cfrac{1}{2} \cfrac{m_A}{m_B} q_{s1} q_{s2} + \cfrac{1}{2} \cfrac{m_A}{m_B} Q_a^2 \cot \alpha \right) \\ & \times \sin \alpha \cos \alpha \\ =& \left[ \left(\cfrac{1}{2} + 2\cfrac{m_A^2}{m_B^2} + 2\cfrac{m_A}{m_B} \right) \sin^2 \alpha + \cfrac{1}{2}\cot^2\alpha \cos^2 \alpha + \left( 1 + 2 \cfrac{m_A}{m_B}\right) \cot \alpha \sin \alpha \cos \alpha \right]Q_a^2 \\ & + q_{s1}^2 \cfrac{1}{2}\sin^2 \alpha \\ & + q_{s2}^2 \left(\cfrac{1}{2} + 2\cfrac{m_A^2}{m_B^2} + 2\cfrac{m_A}{m_B} \right) \cos^2 \alpha \\ & + q_{s1} q_{s2} \left(1 + \cfrac{2m_A}{m_B} \right) \sin \alpha \cos \alpha \\ =& \left[ \left(\cfrac{1}{2} + 2\cfrac{m_A^2}{m_B^2} + 2\cfrac{m_A}{m_B} \right) \sin^2 \alpha + \cfrac{1}{2}\cot^2\alpha \cos^2 \alpha + \left( 1 + 2 \cfrac{m_A}{m_B}\right) \cos \alpha \sin \alpha \cos \alpha \right]Q_a^2 \\ & + q_{s1}^2 \cfrac{1}{2}\sin^2 \alpha \\ & + q_{s2}^2 \cfrac{\mu^2}{2m_B^2} \cos^2 \alpha \\ & + q_{s1} q_{s2} \cfrac{\mu}{m_B} \sin \alpha \cos \alpha \end{align}

\(Q_a^2\)の係数は次のように簡単にできます(最終形が分かってないと導出は難しいでしょうね…):

\begin{align} & \left(\cfrac{1}{2} + 2\cfrac{m_A^2}{m_B^2} + 2\cfrac{m_A}{m_B} \right) \sin^2 \alpha + \cfrac{1}{2}\cot^2 \alpha \cos^2 \alpha + \left( 1 + 2 \cfrac{m_A}{m_B}\right) \cot \alpha \sin \alpha \cos \alpha \\ = & \cfrac{1}{2m_B^2\sin^2 \alpha} \left[ \left(\cfrac{1}{2} + 2\cfrac{m_A^2}{m_B^2} + 2\cfrac{m_A}{m_B} \right) 2m_B^2 \sin^4 \alpha + m_B^2 \cot^2\alpha \cos^2 \alpha \sin^2 \alpha + 2m_B^2 \left( 1 + 2 \cfrac{m_A}{m_B}\right) \cot \alpha \sin \alpha \cos \alpha \sin^2 \alpha \right] \\ = & \cfrac{1}{2m_B^2\sin^2 \alpha} \left[ \left(m_B^2 + 4 m_A^2 + 4 m_A m_B \right) \sin^4 \alpha + m_B^2 \cos^4\alpha + 2 \left( m_B^2 + 2 m_A m_B \right) \cos^2 \alpha \sin^2 \alpha \right] \\ = & \cfrac{1}{2m_B^2\sin^2 \alpha} \left[ m_B^2 (\sin^4 \alpha + 2\cos^2\alpha \sin^2 \alpha + \cos^4 \alpha) + 4 m_A^2 \sin^4 \alpha + 4 m_A m_B (\sin^4 \alpha + \cos^2 \alpha \sin^2 \alpha) \right] \\ = & \cfrac{1}{2m_B^2\sin^2 \alpha} \left[ m_B^2 (\sin^2 \alpha + \cos^2 \alpha)^2 + 4 m_A^2 \sin^4 \alpha + 4 m_A m_B \sin^2 \alpha \right] \\ = & \cfrac{1}{2m_B^2\sin^2 \alpha} \left[ m_B^2 + 4 m_A m_B \sin^2 \alpha + 4 m_A^2 \sin^4 \alpha \right] \\ = & \cfrac{1}{2m_B^2\sin^2 \alpha} \left( m_B + 2 m_A \sin^2 \alpha \right)^2 \\ = & \cfrac{1}{2 } \left( \cfrac{1}{\sin^2 \alpha} + 2 \cfrac{m_A}{m_B} \right) \left( 1 + 2 \cfrac{m_A}{m_B} \sin^2 \alpha \right) \\ \end{align}

最終的に\(U_1\)は次のようになります:

\begin{align} U_1 & = \cfrac{k_1}{2} \left[ Q_a^2 \cfrac{1}{2 } \left( \cfrac{1}{\sin^2 \alpha} + 2 \cfrac{m_A}{m_B} \right) \left( 1 + 2 \cfrac{m_A}{m_B} \sin^2 \alpha \right) + q_{s1}^2 \cfrac{1}{2}\sin^2 \alpha + q_{s2}^2 \cfrac{\mu^2}{2m_B^2} \cos^2 \alpha + q_{s1} q_{s2} \cfrac{\mu}{m_B} \sin \alpha \cos \alpha \right] . \end{align}

ラグランジアン

長くなりましたが、最終的にラグランジアンは次のようになります:

\begin{align} L = & \cfrac{m_A}{4} \dot{q}_{s1}^2 + \cfrac{m_A \mu }{4} \dot{q}_{s2}^2 + \cfrac{m_A}{4} \left( \cfrac{2m_A}{m_B} + \cfrac{1}{\sin^2\alpha} \right) \dot{Q}_{a}^2 \\ & – \cfrac{k_2}{2} (q_{s1}^2\cos^2 \alpha + \cfrac{\mu^2}{m_B^2} q_{s2}^2 \sin^2 \alpha – 2 q_{s1}q_{s2} \cfrac{\mu}{m_B} \sin \alpha \cos \alpha )\\ &- \cfrac{k_1}{2} \left[ Q_a^2 \cfrac{1}{2 } \left( \cfrac{1}{\sin^2 \alpha} + 2 \cfrac{m_A}{m_B} \right) \left( 1 + 2 \cfrac{m_A}{m_B} \sin^2 \alpha \right) + q_{s1}^2 \cfrac{1}{2}\sin^2 \alpha + q_{s2}^2 \cfrac{\mu^2}{2m_B} \cos^2 \alpha + q_{s1} q_{s2} \cfrac{\mu}{m_B} \sin \alpha \cos \alpha \right] \\ = & \cfrac{m_A}{4} \left( \cfrac{2m_A}{m_B} + \cfrac{1}{\sin^2\alpha} \right) \dot{Q}_{a}^2 \cfrac{m_A}{4} \dot{q}_{s1}^2 + \cfrac{m_A \mu }{4} \dot{q}_{s2}^2 \\ & – Q_a^2 \cfrac{k_1}{4 } \left( \cfrac{1}{\sin^2 \alpha} + 2 \cfrac{m_A}{m_B} \right) \left( 1 + 2 \cfrac{m_A}{m_B} \sin^2 \alpha \right) \\ & – q_{s1}^2 \cfrac{1}{4}\left(k_1 \sin^2 \alpha + 2 k_2 \cos^2 \alpha \right) \\ & – q_{s2}^2 \cfrac{\mu^2}{4m_B^2} \left(k_1 \cos^2 \alpha + 2 k_2 \sin^2 \alpha \right) \\ & – q_{s1} q_{s2} \cfrac{\mu}{2m_B}\left(k_1 – 2k_2 \right) \sin \alpha \cos \alpha .\\ \end{align}

振動数の計算

\(Q_a\)

\(Q_a\)については変数が独立になっています。これから単純に

\[ \omega_a^2 = \cfrac{k_1}{m_A} \left( 1 + 2 \cfrac{m_A}{m_B} \sin^2 \alpha \right). \]

\(q_{s1}\), \(q_{s2}\)

\(q_{s1}\), \(q_{s2}\) については運動方程式を解きます。

\begin{align} q_{s1} = & A_{s1}e^{i\omega t} \\ q_{s2} = & A_{s2}e^{i\omega t} \end{align}

と置いてラグランジアンに代入します:

\begin{align} -\omega^2 \cfrac{m_A}{2} A_{s1} + A_{s1} \cfrac{1}{2}\left(k_1 \sin^2 \alpha + 2k_2\cos^2 \alpha \right) + A_{s2} \cfrac{\mu}{2m_B}\left(k_1 – 2k_2 \right) \sin \alpha \cos \alpha = & 0 \\ -\omega^2 \cfrac{m_A\mu}{2m_B} A_{s2} + A_{s2} \cfrac{\mu^2}{2m_B} \left(k_1 \cos^2 \alpha + 2 k_2 \sin^2 \alpha \right) + A_{s1} \cfrac{\mu}{2m_B^2}\left(k_1 – 2k_2 \right) \sin \alpha \cos \alpha = & 0. \end{align}

これを整理します:

\begin{align} \left[ -\omega^2 \cfrac{m_A}{2} + \cfrac{1}{2}\left(k_1 \sin^2 \alpha + \cos^2 \alpha \right) \right] A_{s1} & + \left[ \cfrac{\mu}{2m_B}\left(k_1 – 2k_2 \right) \sin \alpha \cos \alpha \right] A_{s2} = & 0 \\ \left[ \cfrac{\mu}{2m_B}\left(k_1 – 2k_2 \right) \sin \alpha \cos \alpha \right] A_{s1} & + \left[ -\omega^2 \cfrac{m_A\mu}{2m_B} + \cfrac{\mu^2}{2m_B^2} \left(k_1 \cos^2 \alpha + 2 k_2 \sin^2 \alpha \right)\right] A_{s2} = & 0. \end{align}

あるいは(いくつか約分して)

\begin{align} \left[ -\omega^2 m_A + \left(k_1 \sin^2 \alpha + \cos^2 \alpha \right) \right] A_{s1} & + \left[ \cfrac{\mu}{m_B}\left(k_1 – 2k_2 \right) \sin \alpha \cos \alpha \right] A_{s2} = & 0 \\ \left[ \cfrac{\mu}{m_B}\left(k_1 – 2k_2 \right) \sin \alpha \cos \alpha \right] A_{s1} & + \left[ -\omega^2 \cfrac{m_A\mu}{m_B} + \cfrac{\mu^2}{m_B^2} \left(k_1 \cos^2 \alpha + 2 k_2 \sin^2 \alpha \right)\right] A_{s2} = & 0. \end{align}

これから特性方程式をつくると次のようになります:

\begin{align} \cfrac{m_A^2\mu}{m_B} \omega^4 & \\ – \left[ \cfrac{m_A \mu^2}{m_B^2} \left(k_1 \cos^2 \alpha + 2 k_2 \sin^2 \alpha \right) + \cfrac{m_A \mu}{m_B} \left(k_1 \sin^2 \alpha + 2k_2\cos^2 \alpha \right) \right] \omega^2 & \\ + \cfrac{\mu^2}{m_B^2} \left(k_1 \sin^2 \alpha + 2k_2\cos^2 \alpha \right) \left(k_1 \cos^2 \alpha + 2 k_2 \sin^2 \alpha \right) &\\ – \cfrac{\mu^2}{m_B^2}\left(k_1 – 2k_2 \right)^2 \sin^2 \alpha \cos^2 \alpha &= 0 \end{align}

\(\omega^2\)の係数は

\begin{align} & – \left[ \cfrac{m_A \mu^2}{m_B^2} \left(k_1 \cos^2 \alpha + 2 k_2 \sin^2 \alpha \right) + \cfrac{m_A \mu}{m_B} \left(k_1 \sin^2 \alpha + 2k_2\cos^2 \alpha \right) \right] \\ = & – \cfrac{m_A \mu}{m_B}\left[ \cfrac{ \mu}{m_B} \left(k_1 \cos^2 \alpha + 2 k_2 \sin^2 \alpha \right) + \left(k_1 \sin^2 \alpha + 2k_2\cos^2 \alpha \right) \right] \\ = & – \cfrac{m_A \mu}{m_B}\left[ k_1 \left( \sin^2 \alpha + \cfrac{\mu}{m_B} \cos^2 \alpha \right) + 2 k_2 \left( \cos^2 \alpha + \cfrac{\mu}{m_B} \sin^2 \alpha \right) \right] \\ = & – \cfrac{m_A \mu}{m_B}\left[ k_1 \left( 1 + \cfrac{2m_A}{m_B} \cos^2 \alpha \right) + 2 k_2 \left( 1 + \cfrac{2m_A}{m_B} \sin^2 \alpha \right) \right]. \\ \end{align}

定数項は

\begin{align} & \cfrac{\mu^2}{m_B^2} \left(k_1 \sin^2 \alpha + 2k_2\cos^2 \alpha \right) \left(k_1 \cos^2 \alpha + 2 k_2 \sin^2 \alpha \right) – \cfrac{\mu^2}{m_B^2}\left(k_1 – 2k_2 \right)^2 \sin^2 \alpha \cos^2 \alpha \\ & = \cfrac{\mu^2}{m_B^2}\left[ \left(k_1 \sin^2 \alpha + 2k_2\cos^2 \alpha \right) \left(k_1 \cos^2 \alpha + 2 k_2 \sin^2 \alpha \right) – \left(k_1^2 + 4k_2^2 – 4 k_1 k_2 \right) \sin^2 \alpha \cos^2 \alpha \right] \\ & = \cfrac{\mu^2}{m_B^2}\left[ 2 k_1 k_2 \left( \sin^4 \alpha + \cos^4 \alpha \right) + 4 k_1 k_2 \sin^2 \alpha \cos^2 \alpha \right] \\ & = \cfrac{\mu^2}{m_B^2} 2 k_1 k_2 \left( \sin^2 \alpha + \cos^2 \alpha \right)^2 \\ & = \cfrac{\mu^2}{m_B^2} 2 k_1 k_2 \end{align}

最終的に特性方程式は次のようになります:

\begin{align} \cfrac{m_A^2 \mu}{m_B}\omega^4 – \cfrac{m_A \mu}{m_B}\left[ k_1 \left( 1 + \cfrac{2m_A}{m_B} \cos^2 \alpha \right) + 2 k_2 \left( 1 + \cfrac{2m_A}{m_B} \sin^2 \alpha \right) \right] \omega^2 + \cfrac{\mu^2}{m_B^2} 2 k_1 k_2 = &0 \\ \omega^4 – \left[ \cfrac{k_1}{m_A} \left( 1 + \cfrac{2m_A}{m_B} \cos^2 \alpha \right) + 2 \cfrac{k_2}{m_A} \left( 1 + \cfrac{2m_A}{m_B} \sin^2 \alpha \right) \right] \omega^2 + \cfrac{2 \mu}{m_A^2 m_B} k_1 k_2 = &0 \\ \end{align}

\(2 \alpha = \pi \)の場合

\(\omega_a\)

\[ \omega_a^2 = \cfrac{k_1}{m_A} \left( 1 + 2 \cfrac{m_A}{m_B} \right) = \cfrac{\mu k_1 }{m_A m_B} \]

\(q_{s1}, q_{s2} \)の振動数

\(2 \alpha = \pi \)の場合、特性方程式は次のようになります:

\begin{align} \omega^4 – \left[ \cfrac{k_1}{m_A} + 2 \cfrac{k_2}{m_A} \left( 1 + \cfrac{2m_A}{m_B} \right) \right] \omega^2 + \cfrac{2 \mu}{m_A^2 m_B} k_1 k_2 = &0 \\ \omega^4 – \left[ \cfrac{k_1}{m_A} + 2 \cfrac{k_2\mu }{m_A m_B} \right] \omega^2 + \cfrac{2 \mu}{m_A^2 m_B} k_1 k_2 = &0 \\ \left( \omega^2 – \cfrac{k_1}{m_A} \right) \left( \omega^2 – 2 \cfrac{k_2\mu }{m_A m_B} \right) = &0. \\ \end{align}

これから問題1の振動数の二つが得られます:

\begin{align} \omega & = \sqrt{\cfrac{k_1}{m_A}} \\ \omega & = \sqrt{2 \cfrac{k_2\mu }{m_A m_B} }. \\ \end{align}