(更新日: 2025年9月11日 )
目次
はじめに
Simulinkでモデリングする際に、急激な変化を緩和したい場合や高周波成分を除去したい場合がある。 そんな時はローパスフィルタをモデル上に設ける。 Simulinkでローパスフィルタを作る時は Transfer Fcn(伝達関数)ブロックを使うことがよくある。
今回はその基礎的な内容と実際のSimulinkでの表現例と合わせて紹介しようと思う。 Simulinkモデルに関してはTransfer Fcnブロック以外の表現についても述べた。
ローパスフィルタの理論
その理屈は次のようなものだ。
ローパスフィルタは入力をRC直列回路に入れて、そのCの両端から信号を取り出すイメージ。
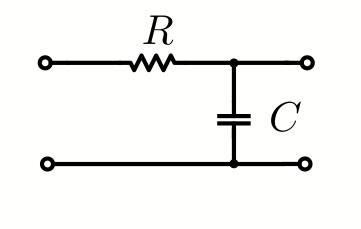
この場合入力電圧をV1、出力電圧をV2とすると
\[ \cfrac{V2}{V1} = \cfrac{\cfrac{1}{j\omega C}}{R + \cfrac{1}{j\omega C}} = \cfrac{1}{1 + j\omega CR} \]となる。\(CR = \tau \)とする。カットオフ周波数を\(\omega_c = 2 \pi f_c\)とすると、周期と周波数の関係から
\[ \tau = \cfrac{1}{2 \pi f_c} \]だ。この回路の伝達関数が欲しいので\(j\omega\)をラプラス変換の \(s\)に入れ替えると
\[ \cfrac{1}{1 + \cfrac{1}{2\pi f_c}s} \]だが、普通は時定数を使うほうが多いから次のように書く:
\[ \cfrac{1}{1 + \tau s}. \]Simulinkモデルの例
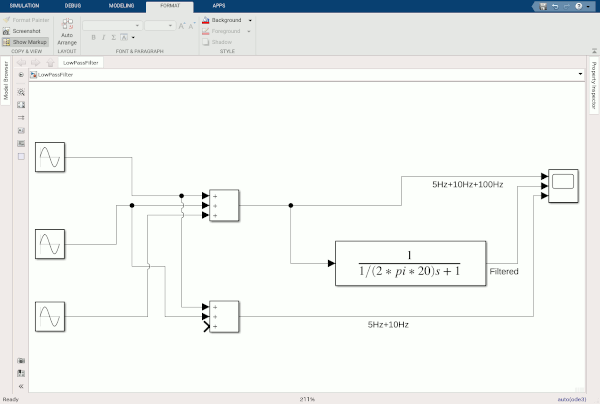
この伝達関数で実際にSimulinkモデルを作ってみた。 Simulinkモデルこちら→ LowPassFilter.zip
フィルタの効果を確認
実際にフィルタの効果を確認してみよう。 具体的にはカットオフ周波数を変えていくと、どのようにフィルタされるかを見ていく。 カットオフ周波数を、200 Hz, 100 Hz, 20 Hz, 5 Hzにしてプロットさせた。
このモデルでは入力信号に5 Hz, 10 Hz, 100 Hzのサイン波を足したものを入れている。
カットオフ周波数=200 Hz
まずは200Hzの場合。信号がほとんど変化しないことが分かる。
信号の最大周波数が100 Hzであるため、それより大きなカットオフ周波数に設定するなら信号はほぼ素通りだ。つまりローパスフィルタとしては機能しない。
カットオフ周波数=100 Hz
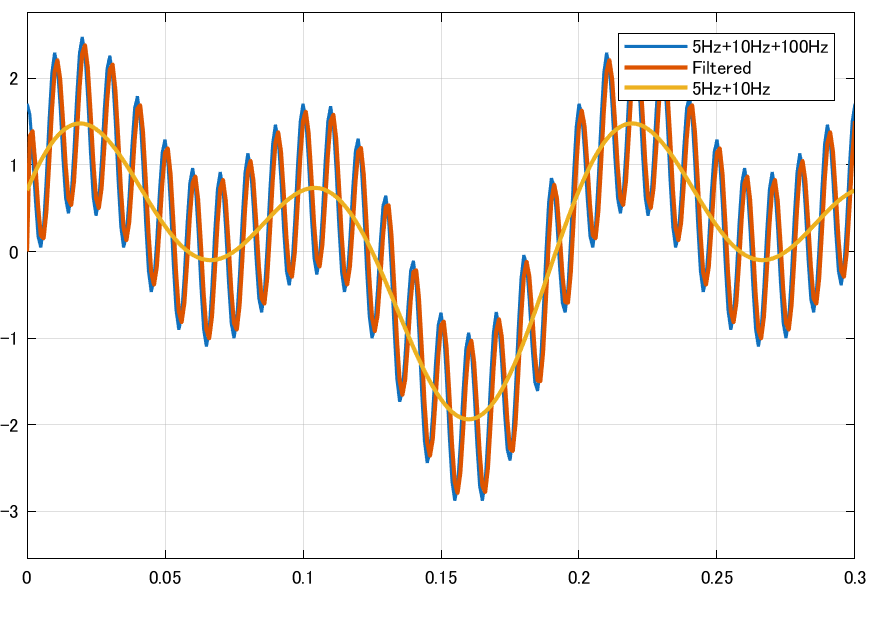
カットオフ周波数を100 Hzにすると、信号の細かい振動(100 Hz成分)の振幅が小さくなるのが分かる。
なおカットオフ周波数において振幅が-3 dB ≒ 0.7倍になる。
カットオフ周波数=20 Hz
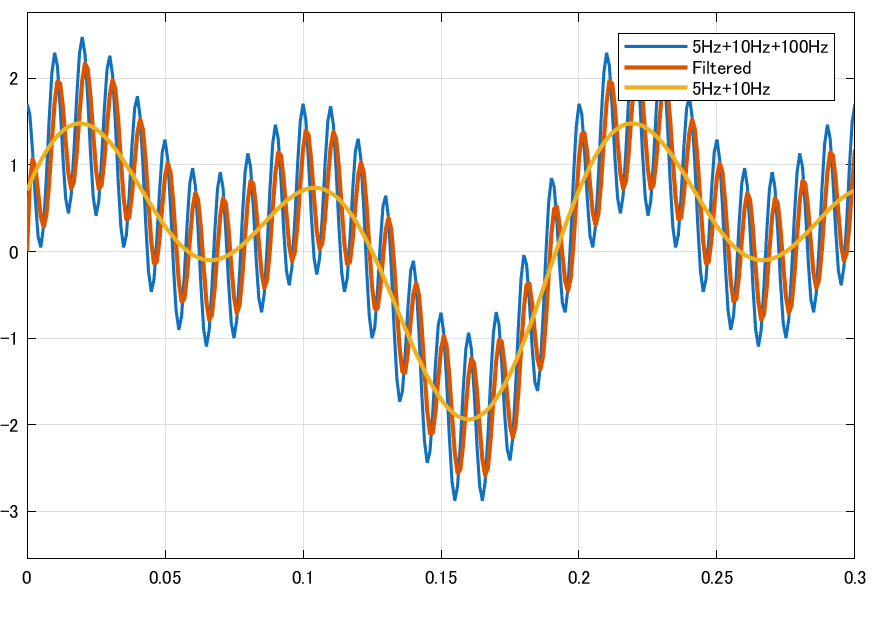
カットオフ周波数を20 Hzにすると、信号の細かい振動(100 Hz成分)の振幅がかなり小さくなる。フィルタが機能している様子が分かりやすい。
また、5 Hz + 10 Hzの信号と比較すると、フィルタされた信号が若干遅れているのが分かる。 これは分母が\(1 + \tau s\)のように\(s\)の1次で表現されている「1次遅れ系」だから。
カットオフ周波数=5 Hz
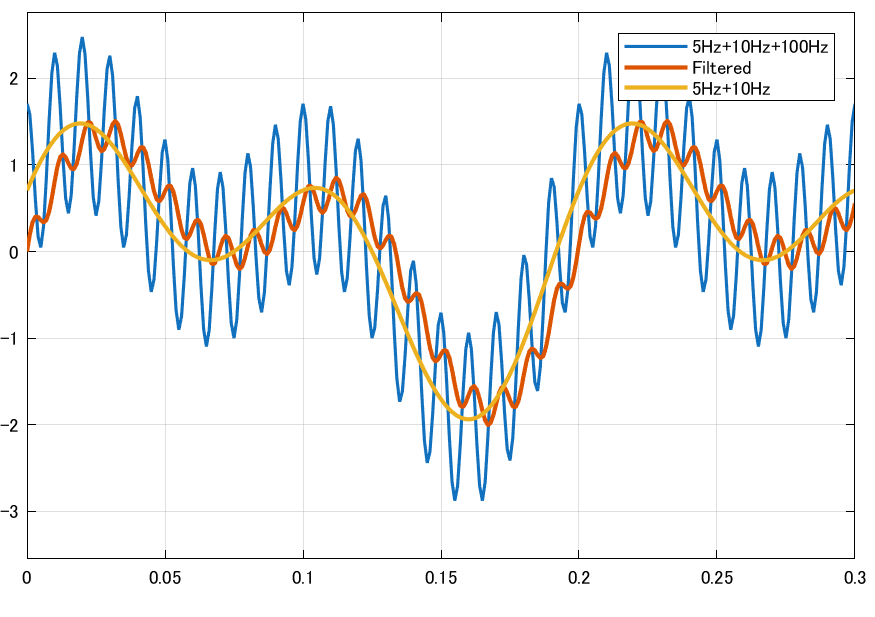
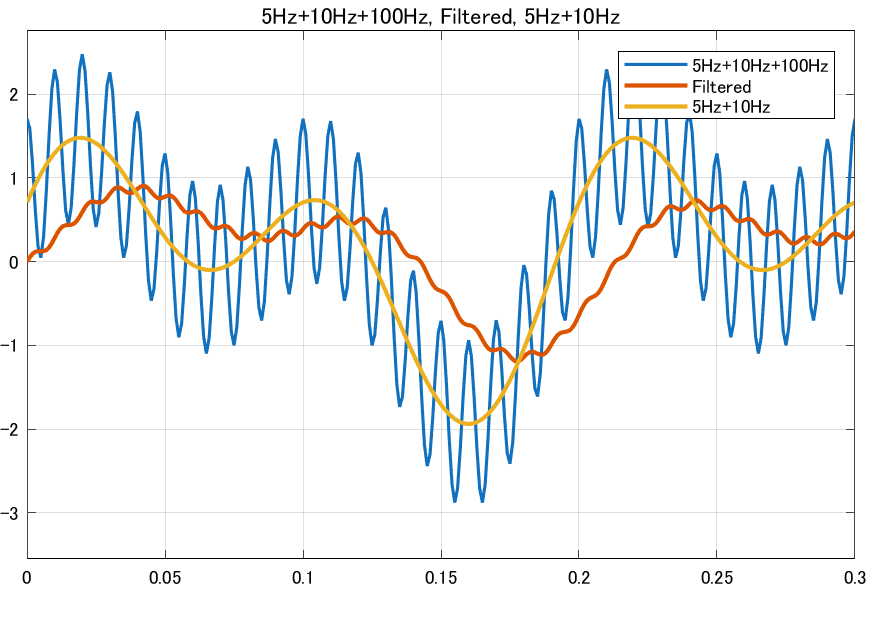
カットオフ周波数を5 Hzにすると、信号の細かい振動(100 Hz成分)の振幅がほとんどなくなる。そして遅れも大きいことが分かる。
伝達関数以外での表現方法
伝達関数を使うのが手軽だが、初期値を設定できないなど不都合な場合もある。そうした時は伝達関数以外で表現する必要がある。 ここでは二つの表現方法を紹介しよう。積分器を使う方法
伝達関数が
\[ \cfrac{1}{1+\tau s} \]の形をしている。ここでブロック線図の等価変換を思い出そう。
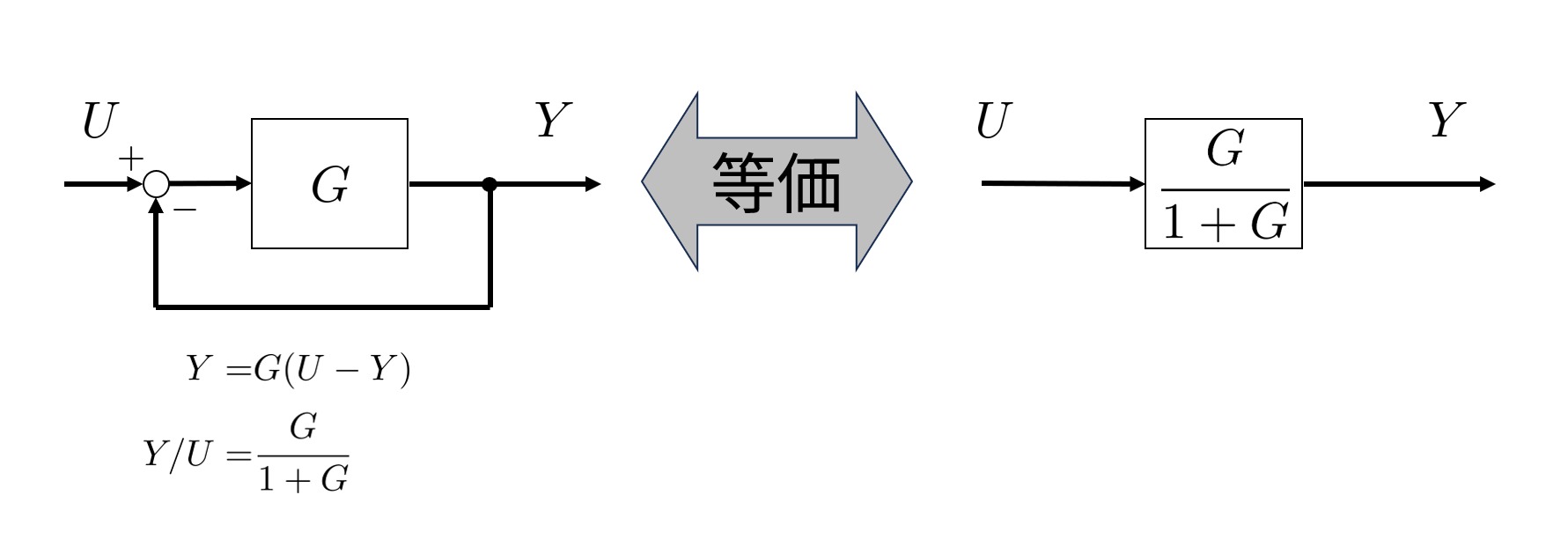
伝達関数\(G\)が負のフィードバック結合している場合、全体の伝達関数は
\[ \cfrac{G}{1+G} \]となる。ここで\(G = 1/(\tau s) \)とすれば、全体の伝達関数が
\[ \cfrac{1}{1+\tau s} \]になることが分かる。これをモデルで表現するなら、\(1/\tau = 2\pi f_c\)のゲインと積分器\(1/s\)を直列にして、負のフィードバック結合すれば良い。
モデルの例が下の図。 Simulinkモデルこちら→ LowPassFilterInteg.zip
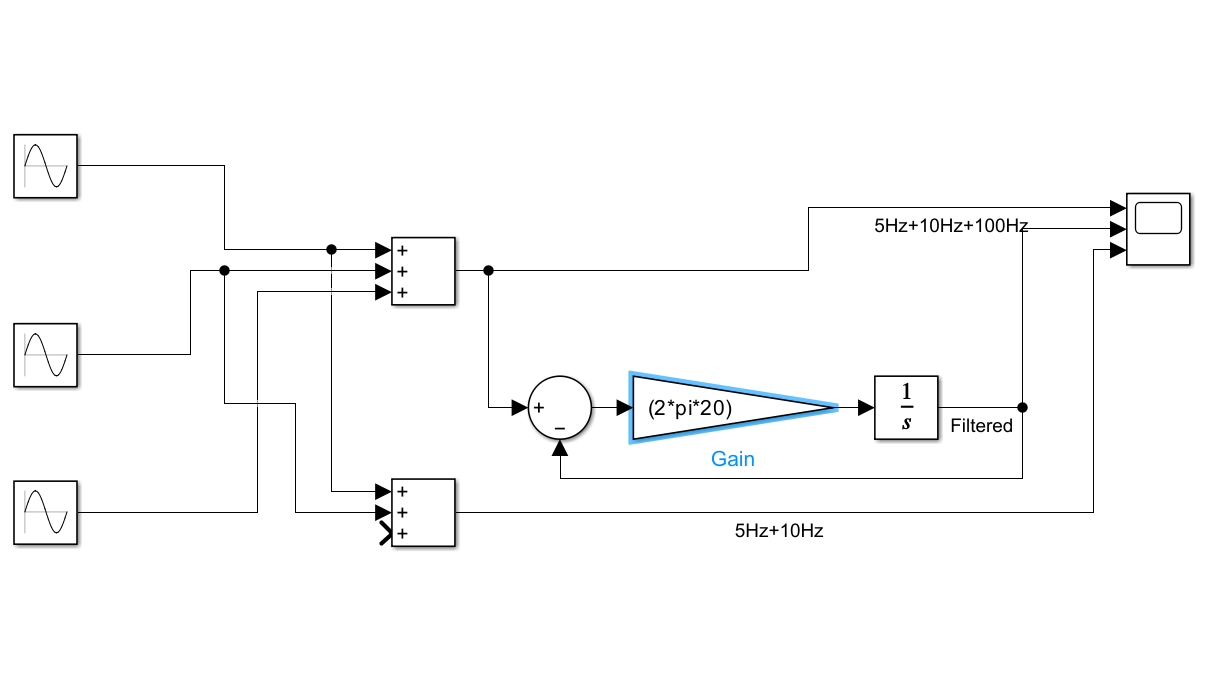
積分器は初期値を設定できるから、ゼロ以外の値が入力されることが分かっているなら、この方法か、次で説明する指数移動平均の方法を用いることになる。
指数移動平均で計算する方法
もう一つの方法が指数移動平均で計算する方法。
指数移動平均とは
RC回路によるローパスフィルタは移動平均の一つである指数移動平均と等価であることが知られている。 指数移動平均とは、移動平均をとる際の重みを指数関数的に減少させるもの。
指数移動平均を数式で表現すると
\[ y[n] = (1-\alpha) y[n-1] + \alpha x[n] \]ここで\(y\)は出力、\(x\)は入力である。\(\alpha\)は平均を計算する時の重みで\(0 \le \alpha \le 1\)。
この式の意味するのは、一つ前の出力値と今の入力値の平均値から出力の平均値を計算していること。 \(0\le \alpha\le 1\)によって、ずっと昔の出力値の重みが小さくなる。
RCローパスフィルタの場合の$\alpha$
では、RCローパスフィルタの時定数と\(\alpha\)の関係を導出しておく。
RCローパスフィルタの微分方程式は以下の通り:
\[ V_1 = CR \cfrac{d V_2}{dt} + V_2. \]\(V_1\)、\(V_2\)はそれぞれ入力電圧、出力電圧だから、これらを制御理論で使われる入力と出力の記号\(u\)、\(y\)に置き換えて、\(RC = \tau\)とする。 こうすると状態方程式の形式に書き直すことが出来る:
\[ \cfrac{dy}{dt} = \cfrac{-1}{\tau} y + \cfrac{1}{\tau} x \]この状態方程式を厳密に離散化をする。
厳密に離散化するとは以下のようなことを言う。まず連続時間の状態方程式
\[ \dot{\boldsymbol{y}}(t) = \boldsymbol{A} \boldsymbol{y}(t) + \boldsymbol{B} \boldsymbol{u}(t) \]を考える。サンプリング時間を$T_s$とした場合、これを厳密に離散化すると以下のように書くことが出来る:
\[ \boldsymbol{y}[k+1] = e^{\boldsymbol{A} T_s} \boldsymbol{y}[k] + \boldsymbol{A}^{-1} \left(e^{\boldsymbol{A} T_s} – \boldsymbol{I}\right) \boldsymbol{B} \boldsymbol{u}[k]. \]さてRCローパスフィルタの状態方程式に戻ると、$A = -1/\tau$, $B = 1/\tau$とすると上の公式が使える。
こうすると離散時間でのRCローパスフィルタの状態方程式は
\[ y[k+1] = e^{- T_s/\tau} y[k] + \left(1 – e^{- T_s/\tau} \right) u[k] \]となり、指数移動平均の式と比較すると$\alpha = 1 – e^{- T_s/\tau} $であることが分かる。
Simulinkモデルの例
上の指数移動平均をSimulinkで表現したの下の図。Simulinkモデルはこちら→ LowPassFilterUnitDelay.zip
gainブロックの中身は、左側、右側はそれぞれ$\alpha = 1 – e^{- T_s/\tau}$、$1 – \alpha =e^{- T_s/\tau}$である。
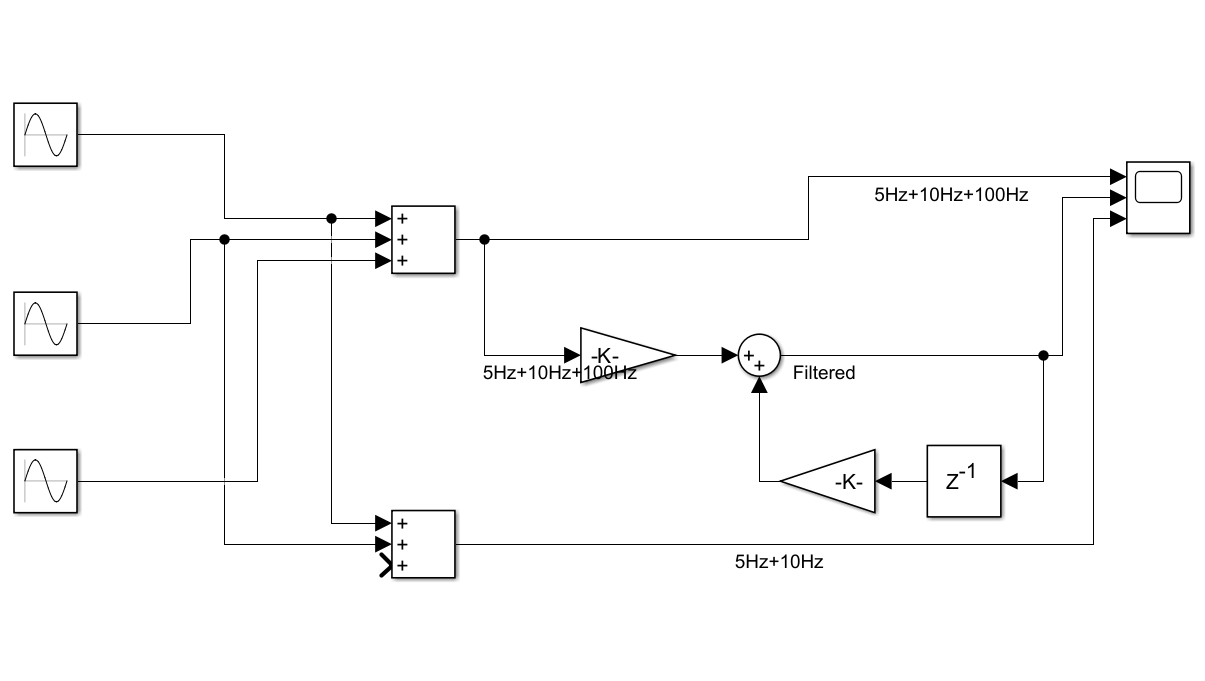
カットオフ周波数を二つのgainブロックで設定するのが煩雑なので、それを書き直したのが下のモデル例。Simulinkモデル例はこちら→ LowPassFilterUnitDelay2.zip
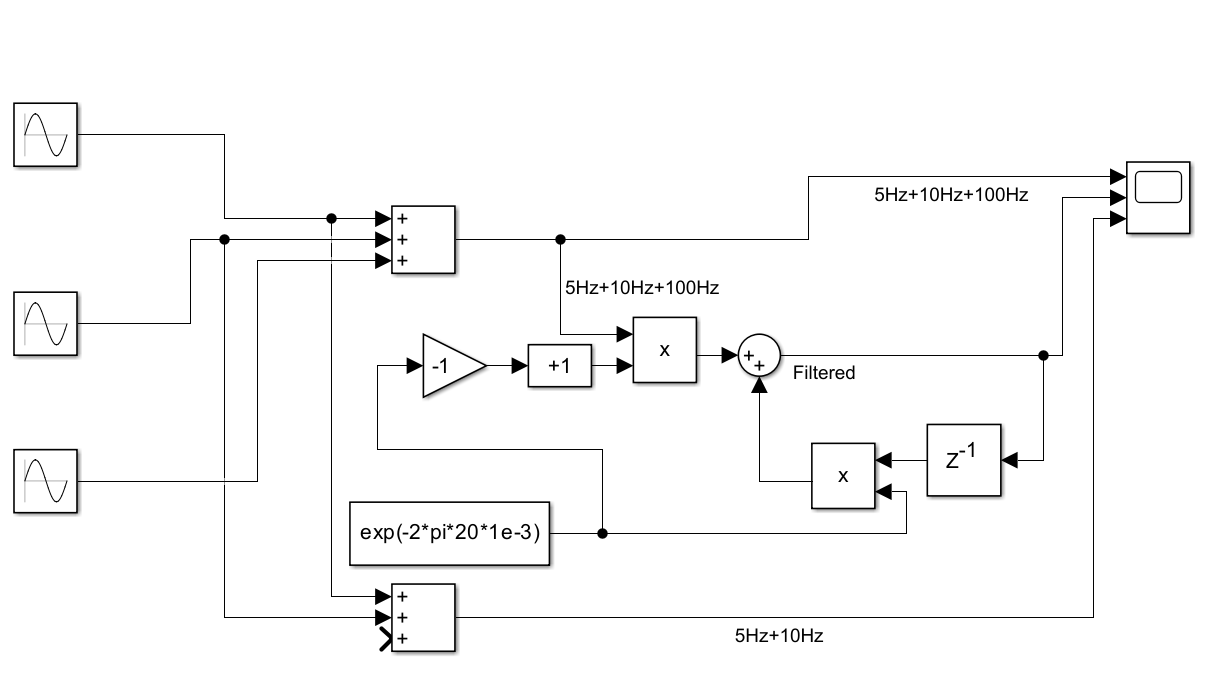
おわりに
RC回路のローパスフィルタを例に、基本的な理論とSimulinkでの表現方法を紹介した。 RC回路のローパスフィルタはアナログ回路であり、方程式も連続時間で表現されていることに注意しよう。
RC回路は一次遅れ系であり、これを離散時間系(デジタル化)で表現するとIIR (Infinite Impulse Response)になる。IIRは上記の指数移動平均になる。 IIRは全てのデータを参照していて、大昔のデータ点の重みは指数関数的に小さくなっている。
一方でFIR (Finite Impulse Response)は有限のデータのみを参照して平均化している。移動平均のイメージ。 厳密には一次遅れ系のローパスフィルタとは違う種族なので、これも注意しよう。
なお、一次遅れ系については一次遅れ系の基礎整理:伝達関数・時定数・周波数特性からSimulinkモデルまでについても参照されたい。