円錐の体積を円柱座標系で真面目に計算してみた

よく知られているように、円錐の体積は

\[ \cfrac{1}{3}\pi R^2 h \]

です。ここで底面の円の半径を\(R\)、高さを\(h\)としました。

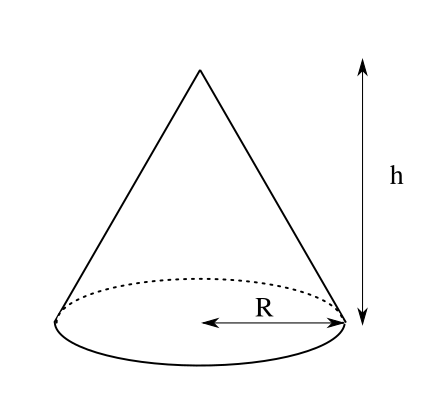
中学の数学などで天下り的に教わったのですが、導出は教わった記憶がありません。ここではその導出をやってみます。

ネットを検索するとよく出てくる方法と、円柱座標系で束縛条件を課してで計算する方法を紹介します。

よくある方法

座標系の選び方

まず座標系を選びましょう。頂点を下側にすると計算が楽です。

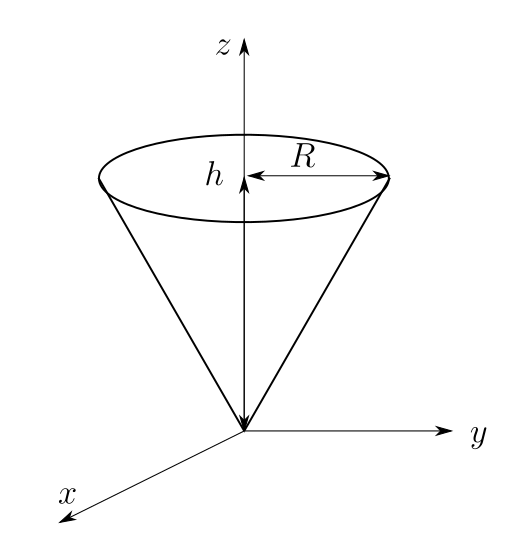
微小な円盤の集合と見て体積を計算する

円錐の体積を計算するには、円錐を微小な厚さの円盤の集合と見立てて計算します。

微小な厚さの円盤の体積を\(\Delta V\)とすると体積は

\[ V = \sum \Delta V \]

という風に書けます。

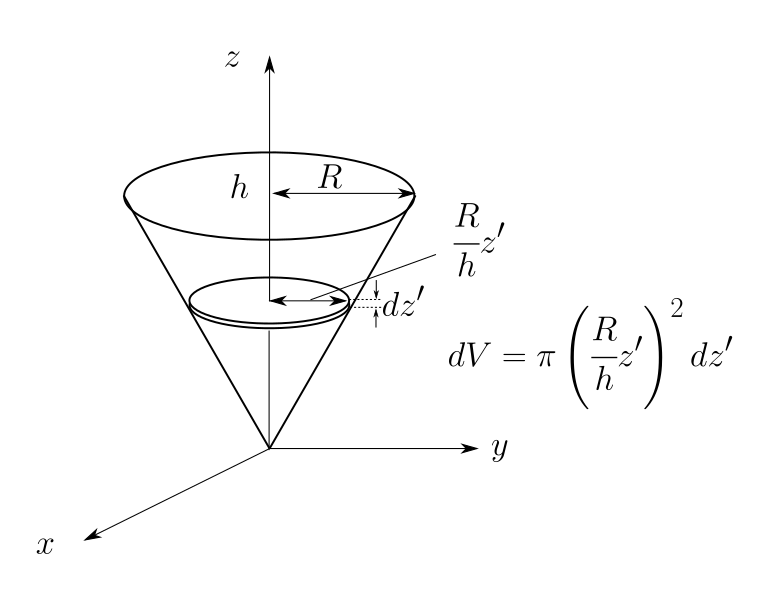
微小な円盤の半径と体積

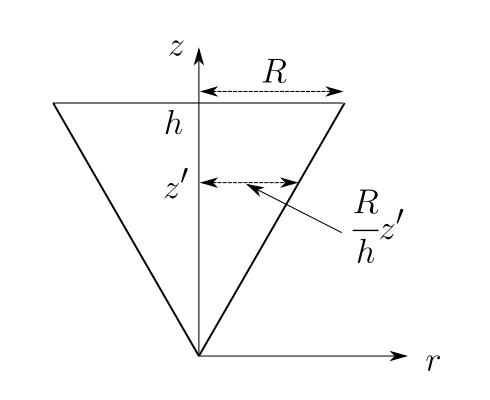
頂点を原点にして、底面に垂直な軸を\(z\)軸にします。こうすると微小な厚さの円盤の半径は\(z\)の関数となります。

具体的には\(z\)のところで切る面の円の半径は

\[ \cfrac{R}{h}z \]

になります。

円の面積は

\[ \pi \left(\cfrac{R}{h}z\right)^2 \]

です。

また円盤の厚さを\(\Delta z\)とすると微小な円盤の体積は

\[ \Delta V = \pi \left(\cfrac{R}{h}z\right)^2 \Delta z \]

です。

円錐の体積の計算

こうして円錐の体積は

\[ V = \sum \Delta V = \sum \pi \left(\cfrac{R}{h}z\right)^2 \Delta z \]

となります。

これをどんどん微小にしていく極限として

\[ V = \int dV = \int \pi \left(\cfrac{R}{h}z\right)^2 d z \]

と書くわけです。\(z\)の範囲は\(0\)から\(h\)までですから

\begin{align} V = & \int_0^h \pi \left(\cfrac{R}{h}z\right)^2 d z \\ = & \pi \cfrac{R^2}{h^2}\int_0^h z^2 d z \\ = & \pi \cfrac{R^2}{h^2} \cfrac{h^3}{3} \\ = & \cfrac{1}{3} \pi R^2 h. \end{align}

こんな感じで導出できます。

この計算の問題は慣性モーメントを計算するときに困る

これが悪いというわけではありませんが、この方法だと慣性モーメントを計算できません。

例えば

\[ I_{z} = \int (x^2+y^2) dV \]

のような積分を円錐内で実行しようとすると、とたんに困難になります。

慣性モーメントが出来るような計算方法を次に説明します。

円柱座標系で積分する方法

円柱座標系の体積要素

円柱座標系での体積要素は

\[ dV = r dr d\theta dz \]

です。

円柱の体積を求めてみると

まず手始めに半径\(R\)、高さ\(h\)の円柱の体積の計算を円柱座標でしてみます。

\(r\)を\(0\)から\(R\), \(\theta\)を0から\(2\pi\), \(z\) を\(0\) から\(h\)まで積分すれば

\begin{align} V_\text{cylinder} & = \int_0^{h} \int_0^{2\pi} \int_0^R r dr d\theta dz \\ & = \left[ \cfrac{r^2}{2}\right]_{r=0}^{r=R} \left[\theta \right]_0^{2\pi} \left[ z \right]_0^h \\ & = \cfrac{R^2}{2} \times 2\pi \times h \\ & = \pi R^2 h \end{align}

となります。底面の面積\(\pi R^2\)と高さ\(h\)の積です。

円錐の体積の計算

では円錐の体積を計算します。円柱の場合と違うのは変数\(r\)の積分が\(z\)に束縛されている点です。そこで\(r\)を\(z\)の関数に変換する必要があります。

母線が\(z\)の関数

\[ r = \cfrac{R}{h}z \]

です。この関係式を使って変数変換とすると

\[ r dr = \left(\cfrac{R}{h}\right)^2 z’ dz’. \]

ここで\(z\)ではなく\(z’\)と書きました(ここがミソ。たぶん)。

\(z’\)を\(0\)から \(z\)まで積分します:

\begin{align} V_\text{cone} =& \int_0^{h} \int_0^{2\pi} \int_0^{z} \left(\cfrac{R}{h}\right)^2 z’ dz’ d\theta dz \\ =& \left(\cfrac{R}{h}\right)^2 \int_0^{h} \int_0^{2\pi} \int_0^{z} z’ dz’ d\theta dz \\ =& \left(\cfrac{R}{h}\right)^2 \int_0^{h} \int_0^{2\pi} \cfrac{1}{2}z^2 d\theta dz \\ =& \cfrac{1}{2} \left(\cfrac{R}{h}\right)^2 \left[ \cfrac{1}{3} z^3\right]_0^h \left[\theta \right]_0^{2\pi} \\ = & \cfrac{1}{2} \left(\cfrac{R}{h}\right)^2 \cfrac{1}{3} h^3 \times 2\pi\\ = & \cfrac{1}{3} \pi R^2 h . \end{align}

意外と簡単に計算できます。