MATLAB・Simulink

一次遅れ系の基礎整理：伝達関数・時定数・周波数特性からSimulinkモデルまで

はじめに

Simulinkでのモデリングでは一次遅れ系を扱うことがとても多い。 なんとなく分かっているようで曖昧なところもあるので、あらためておさらいしてみた。

非常に簡単であるが、MATLABでの応答のプロットやSimulinkでの表現についてもメモした。

一次遅れ系とは

まずは一次遅れ系とは何かをまとめておく。 一次遅れ系（いちじおくれけい）は、制御理論において最も基本的な動的システムの一つで、入力が変化したときに出力が指数関数的に追従していく特性を持つ系である。

一次遅れ系の定義

一次遅れ系とは、次のような微分方程式で表されるシステムを指す:

$$ \tau \frac{dy(t)}{dt} + y(t) = K u(t) $$
  • $u(t)$：入力
  • $y(t)$：出力
  • $K$：定常ゲイン（入力が一定になったときの最終的な比率）
  • $\tau$：時定数（応答速度を決めるパラメータ）

伝達関数

上の一次遅れ系の方程式をラプラス変換すると、伝達関数は次のようになる:

$$ G(s) = \frac{Y(s)}{U(s)} = \frac{K}{\tau s + 1} $$

ここで $s$ はラプラス変数である。

ステップ応答

入力 $u(t)$ が単位ステップ入力（0 から 1 に切り替わる）の場合の出力 $y(t)$ は、

$$ y(t) = K \left(1 – e^{-\frac{t}{\tau}}\right) \quad (t \geq 0) $$

となる。これをプロットしたのが下の図だ:

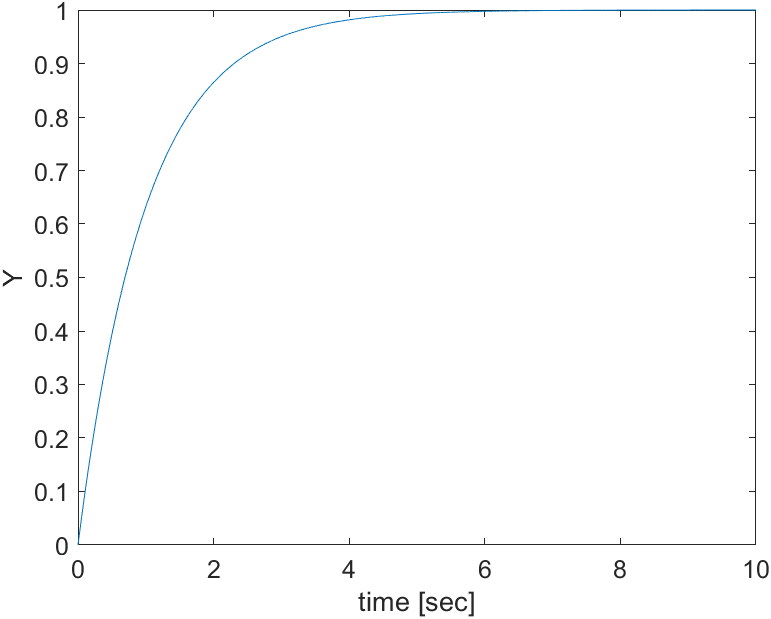
  • $t = \tau$ の時点で、最終値 $K$ の約 63% に到達する。
  • $t = 3\tau$ で約 95%、$t = 5\tau$ でほぼ定常値に収束。

参考: ステップ応答のグラフを生成するMATLABスクリプトの例

f_h_1001 = figure(1001);
plot(timeData, Ydata)
xlabel("time [sec]")
ylabel("Y")
ax = gca;
ax.FontName = "Arial";
ax.FontSize = 12;

exportgraphics(f_h_1001, "firstOrderLagSystem01.png")

特徴

  • なめらかな応答：出力は急激に変化せず、指数関数的に変化する。ただし立ち上がりは不連続に変化する。
  • 時定数 $\tau$：小さいほど応答が速い、大きいほど応答が遅い。
  • ゲイン $K$：入力に対する最終出力の大きさを決定。

具体例

一次遅れ系の具体例はさまざまな物理系で見られる:

  • RC回路（抵抗 $R$ とコンデンサ $C$ の直列回路）：$\tau = RC$
  • 熱伝達系（部屋の温度変化など）：加熱を止めても温度はゆっくり変化
  • 流体タンクの水位制御：流入と流出のバランスで水位が指数的に変化

制御設計上の位置づけ

一次遅れ系は「最もシンプルな動的システム」として、PID制御などの基本的な解析や設計の基礎モデルに使われる。 また、より複雑な高次系や遅れ系も、しばしば一次遅れ系の組み合わせとして近似される。

ボード線図

一次遅れ系のボード線図は下のようになる:

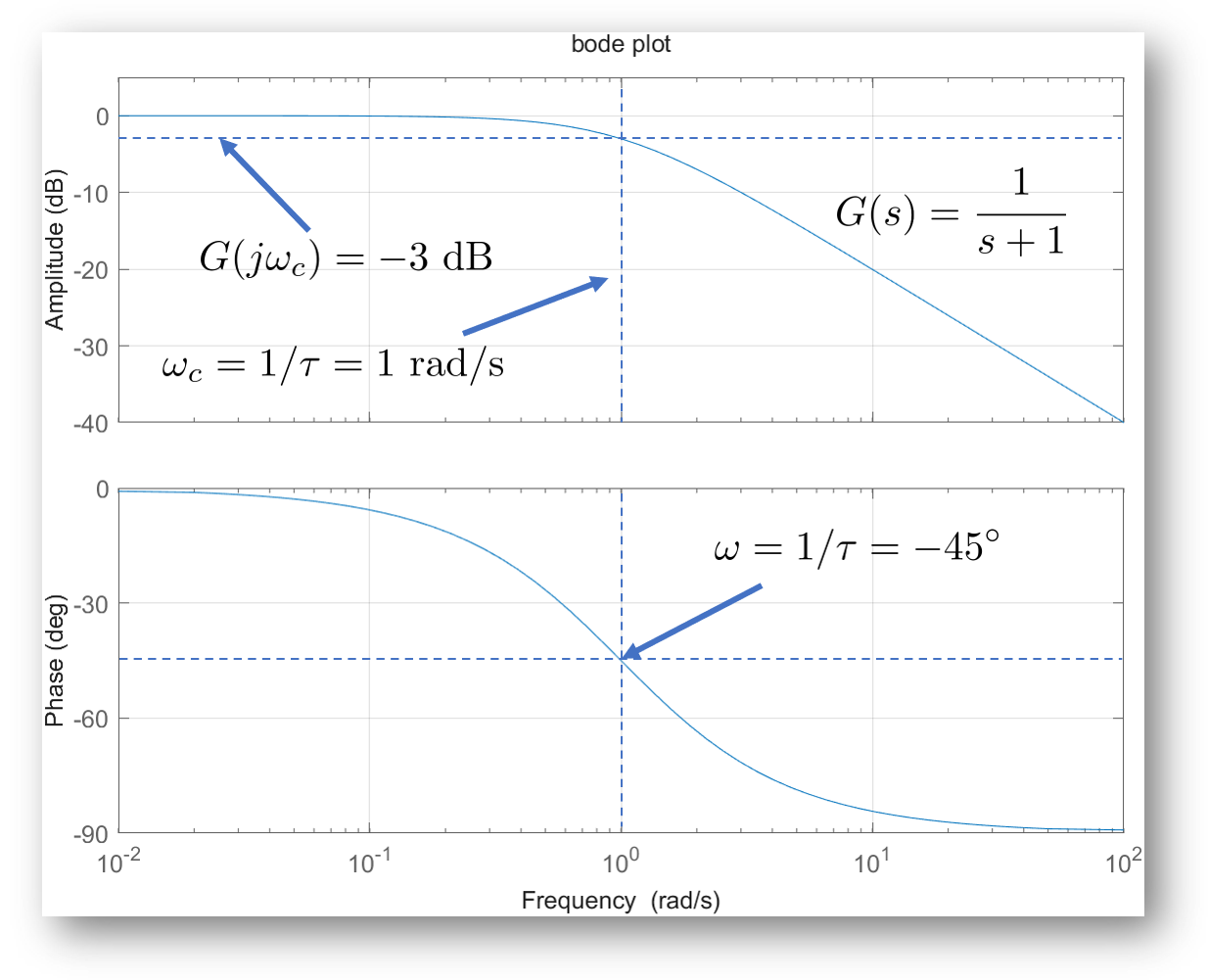
を最短で押さえるポイントは以下の通り:

  • 折れ点（カットオフ）: $\omega_c = 1/\tau = 1 \,\mathrm{rad/s}$ ここでゲインは $-3\,\mathrm{dB}$、位相は $-45^\circ$。
  • 低周波（$\omega \ll 1$）: ゲインは 0 dB（= $K=1$ なのでほぼ等倍）、位相 ~ $0^\circ$。
  • 高周波（$\omega \gg 1$）: ゲイン傾きは $-20\,\mathrm{dB/dec}$、位相は $-90^\circ$ に漸近。

参考: ボード線図を生成するMATLABスクリプトの例

f_h_2001  = figure(2001);
bode(sys)
grid on
ax2 = gca;
ax = findall(f_h_2001, 'type', 'axes');
for ii = 1:numel(ax)
    ax(ii).YLabel.FontSize = 12;
    ax(ii).YLabel.FontName = "Arial";
end
ax(1).YLim = [-40, 5];
ax2.XLabel.FontSize = 12;
ax2.xlabel("Frequency ")
ax2.XLabel.FontName = "Arial";
ax2.Title.FontName  = "Arial";
ax2.Title.FontSize  = 12;
ax2.Title.String    = "bode plot";
ax2.AxesStyle.FontSize = 12;
ax2.AxesStyle.FontName = "Arial";
ax(1).YAxis.Label.String = "Amplitude (dB)";
ax(2).YAxis.Label.String = "Phase (deg)";
exportgraphics(f_h_2001, "firstOrderLagBode.png")

Simulinkモデル

Simulinkで一次遅れ系をモデル化する場合は、Transfer Fcnブロックを使う。モデルはこちら→FirstOrderLagSystem。

とても簡単だが、モデルの例を下図に示しておこう。

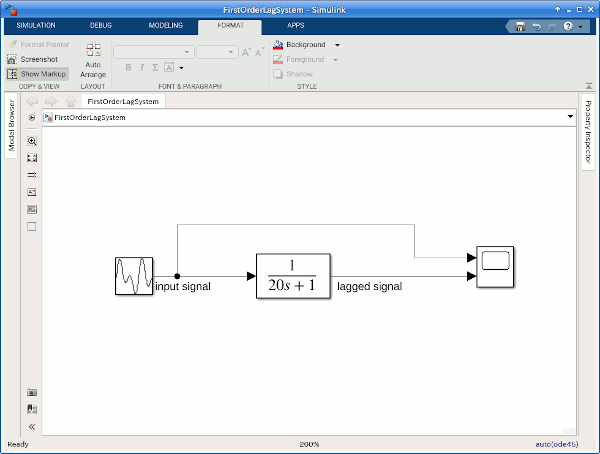
モデルの出力をスコープでモニターした様子が下の図である。

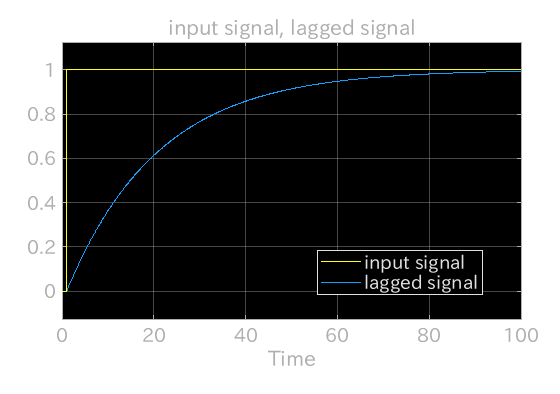
この例ではT=20としている。

上で書いたように、時定数の5倍ほどで、ようやく定常状態に落ち着く。 モデルの例では時定数20秒の5倍、つまり100秒以上経過してようやく出力が1に近くなる。

まとめ

一次遅れ系についておさらいし、MATLABやSimulinkで表現する例を示した。

制御系だけでなく物理系のモデリングでは一次遅れ系を使うことが多い。 特に時定数の設定の感覚を持っておくと便利だろう。

　

RECOMMENDこちらの記事も人気です。