目次
はじめに
電力系の仕事をしていると、有効電力・無効電力というもの遭遇する。
また解析(式計算)をすると
\[ S = \underline{V} \underline{I^*} \]のように、電流の複素共役を電圧に乗じる。
私自身は、このあたりの理解が曖昧だったので自分のために整理してみた。
有効電力と無効電力
交流電圧$v$と電流$i$の瞬時値を次のように書く:
\begin{align*} v(t) = & \sqrt{2}V_\mathrm{rms} \cos(\omega t – \phi) \\ i(t) = & \sqrt{2}I_\mathrm{rms} \cos(\omega t – \phi – \theta) \end{align*}ここで、$\omega = 2\pi f$ で交流の周波数、$\phi$は位相のオフセット、$\theta$は電圧と電流の位相差である。 また、$\theta >$0で電流の位相が電圧より遅れているとする。
なお、$\sin(\omega t – \phi)$とするか、$\cos(\omega t -\phi)$とするかは$\phi$の取り方次第なので、あまり重要ではない。 後で複素平面で議論したいので、ここでは$\cos(\omega t -\phi)$としている。これらを用いて電力の瞬時値p(t)を計算する:
\begin{align} p(t) = & v(t) i(t) \\ = & \sqrt{2}V \cos(\omega t – \phi) \times \sqrt{2}I \cos(\omega t – \phi – \theta) \\ = & 2VI\left\{ \cos(\omega t – \phi) \times \left[ \cos(\omega t – \phi) \cos \theta +\sin(\omega t – \phi) \sin \theta \right] \right\} \tag{1} \\ = & \underbrace{ 2VI \cos\theta \: \cos^2(\omega t – \phi)}_\mathrm{in \: phase} + \underbrace{ 2VI \sin \theta \: \cos(\omega t – \phi)\sin(\omega t – \phi) }_\mathrm{out\: phase} \tag{2} \\ \triangleq & P \: 2 \cos^2(\omega t – \phi) + Q \: 2 \cos(\omega t – \phi)\sin(\omega t – \phi) \end{align}ここで
\begin{align*} P \triangleq & V_\mathrm{rms}\: I_\mathrm{rms} \cos(\theta) \tag{3} \\ Q \triangleq & V_\mathrm{rms}\: I_\mathrm{rms} \sin(\theta) \tag{4} \end{align*}である。
有効電力・無効電力を理解するうえでは、式(2)の書き方が良いと思う。
というのも、電流と電圧の位相差が合っている電力成分の振幅が有効電力、90度の電力成分の振幅が無効電力であることが分かる書き方になっているから。
具体的には、上の式(2)の第一項
\[ 2VI \cos\theta \: \cos^2(\omega t – \phi) \]は電圧の $\cos(\omega t -\phi)$ と同位相の電流成分の積になっている。
一方で第二項
\[ 2VI \sin \theta \: \cos(\omega t – \phi)\sin(\omega t – \phi) \]は 電圧の $\cos(\omega t -\phi)$ と90度位相がずれた電流成分($\sin(\omega t – \phi)$)の積になっている。
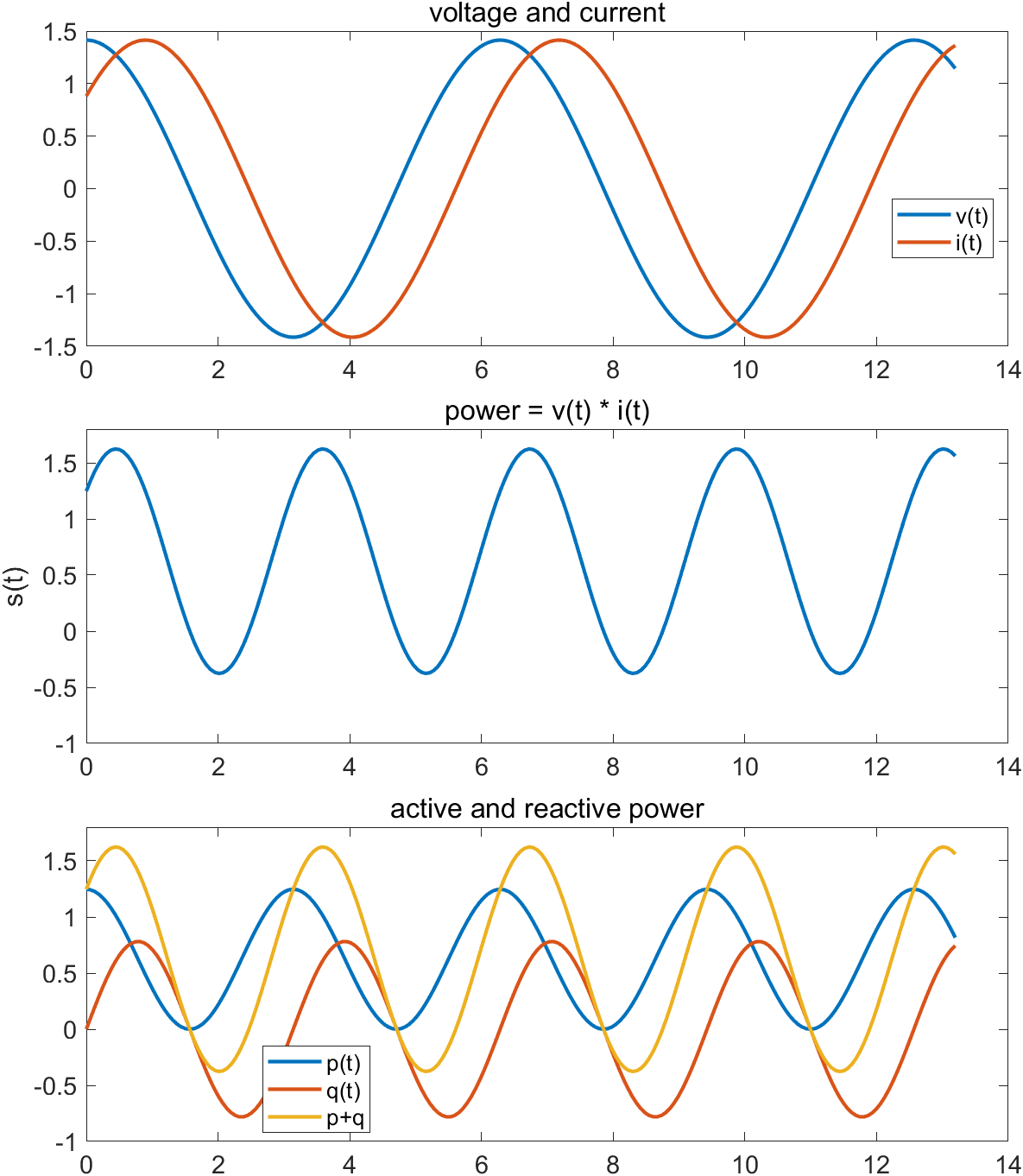
上のグラフは電圧・電流・電力を可視化した例だ。グラフ中の$p(t)$, $q(t)$, $s(t)$はそれぞれ
\begin{align*} p(t) \triangleq & 2V_\mathrm{rms}\: I_\mathrm{rms} \cos\theta \: \cos^2(\omega t – \phi) \\ q(t) \triangleq & 2V_\mathrm{rms}\: I_\mathrm{rms} \sin(\theta) \: \cos(\omega t – \phi)\sin(\omega t – \phi)\\ s(t) \triangleq & v(t) \: \times \:i(t) \end{align*}である。
有効電力・無効電力の意味
上の式(2)を時間平均すると有効電力・無効電力の意味が分かると思う。
実際に時間平均を計算してみよう。$T = 2\pi /\omega$として
\begin{align} \overline{p(t)} = & \cfrac{1}{T}\int_0^T p(t)dt \\ = & VI \cos\theta \: \cfrac{1}{T} \int_0^{T} 2 \cos^2(\omega t – \phi) dt + VI \sin \theta \: \int_0^{T} 2 \cos(\omega t – \phi)\sin(\omega t – \phi) dt \\ = & VI \cos\theta \times 1 + VI \sin \theta \: \times 0 \tag{5} \end{align}となる。
式(5)の第一項の1にかかる係数が有効電力、第二項のゼロにかかる係数が無効電力と呼ばれるものである。
時間平均でゼロにならない電力成分の係数が有効電力、時間平均でゼロになる成分の係数が無効電力ということになる。 「係数」というのがミソで、電力の瞬時値の時間に依存しない係数のことをそれぞれ有効電力・無効電力と呼んでいる。 つまり無効電力に関係する電力成分は瞬時値としては非ゼロの値として存在する。
複素電力との関係
上の式(2)で
- 有効電力は電圧と電流の位相があっている成分どうしの積の時間に依存しない係数
- 無効電力は電圧と電流の位相が90度ずれている成分どうしの積の時間に依存しない係数
- 有効電力・無効電力は電圧と電流の実効値と位相差で表現される
ことを見た。
「位相が90度ずれている」のは複素平面では直交している成分として表現できる。
こうなると、電力を複素数で扱うフェーザ解析と関連づけたくなる。
複素数で表現した交流電圧$\underline{V(t)}$と電流$\underline{I(t)}$の瞬時値を次のように書く:
\begin{align*} \underline{V(t)} = & V_\mathrm{rms} e^{j(\omega t – \phi)} \tag{6}\\ \underline{I(t)} = & I_\mathrm{rms} e^{j(\omega t – \phi – \theta)} \tag{7} \end{align*}(式(6)と(7)は瞬時値の複素表記であり、一方でフェーザの形式は時間因子を含まない)
上述のように有効電力・無効電力は電圧・電流の位相差に依存する。
式(6)と(7)の位相差を取り出すには$\underline{V(t)}$か$\underline{I(t)}$のどちらかの複素共役をとる必要がある。 $\underline{V(t)}$に対して$\underline{I(t)}$の位相を引き算するのであれば$\underline{I(t)}$の複素共役をとることになる。
この積を複素電力$S$とする:
\[ S = \underline{V(t)} \underline{I(t)^*} \tag{8} \]$S$が実際どのようになるかを見てみよう:
\begin{align*} S = & \underline{V(t)} \underline{I(t)^*} \\ = & V_\mathrm{rms} e^{j(\omega t – \phi)} \times I_\mathrm{rms} e^{-j(\omega t – \phi – \theta)} \\ = & V_\mathrm{rms} I_\mathrm{rms} e^{j\theta} \\ = & V_\mathrm{rms} I_\mathrm{rms} \cos\theta + j V_\mathrm{rms} I_\mathrm{rms} \sin\theta \\ = & P + j Q \end{align*}$P$,$Q$ の定義は式(3), (4)にある。
ということで、式(8)の計算でめでたく複素電力が得られた。
なぜ電流の複素共役を乗じるのか
複素電力の計算では、電流の複素共役を電圧に乗じる。この理由は、上で述べたように、位相差を取り出すためと理解するのが良さそうだ。 ネットでもおおむね、このような理解をしている人が多いように思われる。
電圧の複素共役と電流を乗じることもアリだが、どちらを基準にして位相差を計算するかの違いである。慣習的には電流の複素共役を乗じるようだ。
おわりに
瞬時値で有効電力・無効電力を眺めて、今回はようやく腑に落ちた気がする。
フェーザ解析や複素電力だけで考えると、有効電力・無効電力を理解しずらいように、個人的には感じる。 数式が苦手でなければ、面倒がらずに瞬時値の表式をながめるだけでも無効電力の意味を理解できるのではないだろうか。
複素電力での複素共役の扱いについても同様で、瞬時値の表式が頭に入っていれば、それほど難解でもないように思えた。
一方で、私が慣れている理論物理学と比較すると、フェーザ解析・複素電力などは道具立ての側面が強く、物理的な意味付けを突き詰めようとすると袋小路に入ってしまうように感じる。 これが多くの人が「なんで複素共役?」と疑問に思う理由の一つではないか。
特に有効電力が実数成分、無効電力が虚数成分というのは、電圧・電流を複素平面で扱う数学的な道具立て上の決め事や便利な使い方の帰結であって、「なんで?」という疑問にクリアカットな答は難しいように思う。時間平均がゼロの量を虚数で扱うというのは、数学として、あるいは複素平面上では美しいが、これだけを見ると物理的な意味は捉えられない。 こうした部分がいかにも「工学」という分野ということだろうか。














