ランダウ・リフシッツの力学(増補第3版) §32 問題9 のメモです。 図のように慣性軸をとります。 \begin{align} \Omega_1 & = \dot{\theta} \cos \varphi\\…

ランダウ・リフシッツの力学(増補第3版) §32 問題7 のメモです。 OAと慣性中心までの距離が\(a \sin \alpha\)ですから、それに角速度を乗じたものが\(Z\)軸の回転の速度と等しいとおきます: \be…

ランダウ・リフシッツの力学(増補第3版) §32 問題8 のメモです。 問題8を解く 問題7と同様に「回転の角速度は、瞬間的な軸OAの周りの真正の回転の速さとして計算される」と考えます。 OAと慣性中心までの距離が\(a…

ランダウ・リフシッツの力学(増補第3版) §32 問題1 a のメモです。 直線をz軸にとります。 慣性中心\(z_0\)は \[ z_0 = \cfrac{1}{\mu} \sum_a m_a z_a \] ここで\(…

ランダウ・リフシッツの力学(増補第3版) §32 問題3のメモです。 物理振り子(実体振り子)の様子を下のように考えます: ポテンシャル・エネルギーは \begin{align} U & = \mu g l (…

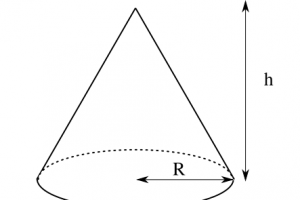
よく知られているように、円錐の体積は \[ \cfrac{1}{3}\pi R^2 h \] です。ここで底面の円の半径を\(R\)、高さを\(h\)としました。 中学の数学などで天下り的に教わったのですが、導出は教わっ…

ランダウ・リフシッツの力学(増補第3版) §29 問題のメモです。 今回は少し分からない部分があります。 まずは \[ \gamma \approx 3\omega_0 \] を \[ \gamma = 3\omega_…

ランダウ・リフシッツの力学(増補第3版) §27 問題2のメモです。 今回は計算すれば割と簡単にフォローできます。 \[ \gamma = \omega_0 + \varepsilon \] として運動方程式 \begi…

ランダウ・リフシッツの力学(増補第3版) §24 問題2のメモです。 今回も長いです。こんなに長くかかるとは思いませんでした(涙目)。 ランダウ先生には怒られそうですが、今回もMaximaを使って検算しましたよ。Stra…

ランダウ・リフシッツの力学(増補第3版) §24 問題2のメモです。 (今回は長いです。こんなに長くかかるとは思いませんでした(涙目)。) 式(24.1)から \begin{align} m_A(x_1 + x_3) +…