buck converterのシミュレーションをしようとインダクタンスや容量にいい加減な値を入れてうまくいかない経験はないか。
自分は多々ある。buck converterに限らずスイッチング・コンバーターの実務経験がないので数値的な感覚がない。
手近な教科書にも実際の数値例はほとんど載っていない。
目次
インダクタンスの設計式
インダクタンスの設計の式がANALOG DEVICESのページにある。(DC/DCレギュレータのインダクタで生じる電流リップル、その許容値はどのようにして決めればよいのか? | アナログ・デバイセズ)
そこでは以下の式が載せてある:
\[ L = \cfrac{V_\mathrm{OUT} \times (1-D) \times T }{CR \times I_\mathrm{OUT}} \]上式で、$V_\mathrm{OUT}$, $I_\mathrm{OUT}$はそれぞれ出力の電圧と電流、そして $L$, $D$, $T$はそれぞれインダクタンス、デューティー比、スイッチング周期、さらに $CR$ はリプル比(率)だ。ここのCRはコンデンサーと抵抗のCR定数ではないことに注意が必要。
このANALOG DEVICESのページでは、上の式の導出は省略されている。
自分は、この手の式の導出がないまま使うのがとても気持ちが悪い。ということで、導出についてメモしておく。
参考になるのはAN-1197 Selecting Inductors for Buck Converters | TEXAS INSTRUMENTSというアプリケーション・ノート。
このアプリケーション・ノートでは、ダイオードやスイッチでの電圧降下も考慮していて、雑な理解には少しばかり煩雑と自分は感じた。 下では、かなり簡略化して上のANALOG DEVICESのページで示されたコンダクタンスの設計式の導出に限定してみた。
以下の導出は電流連続モード(CCM)を想定している。 電流不連続モード(DCM)の場合は入出力電圧が単純なデューティー比ではなくなるので、以下の導出が妥当ではない。
インダクタンスの設計式を導出する
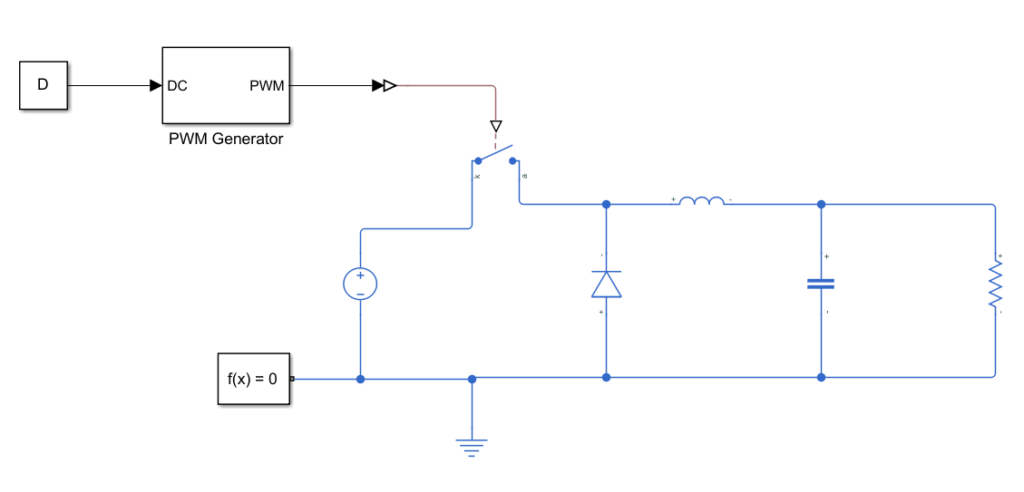
まずbuck converterの構成を下に示す。
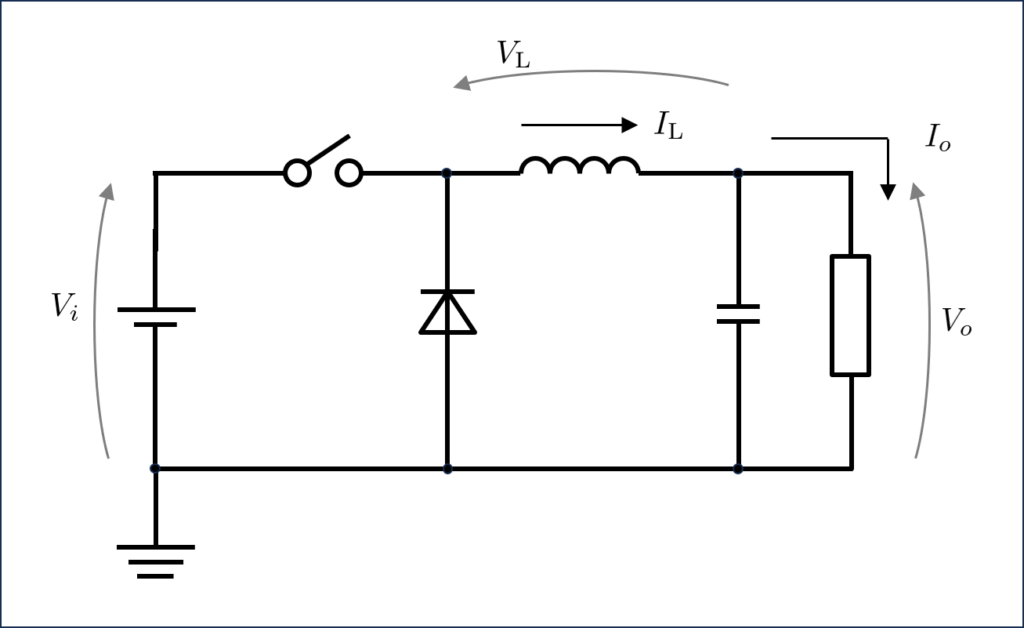
Viは入力電圧値で、負荷側が電圧値がVoになるとする。 入力電源とインダクターの間に挿入されている。インダクターとスイッチの間にダイオードのカソードが接続され、アノードはグラウンドに接続される。 インダクターの入力とは反対側が出力になり、出力には平滑化のコンデンサがグラウンドとの間に接続される。
インダクターの電流$I_\mathrm{L}$はスイッチをon/offすることで増減する。スイッチをonする間は$I_\mathrm{L}$が増加し、offの間は減少する。 その増減幅(量)を$\Delta I_\mathrm{L}$とする。
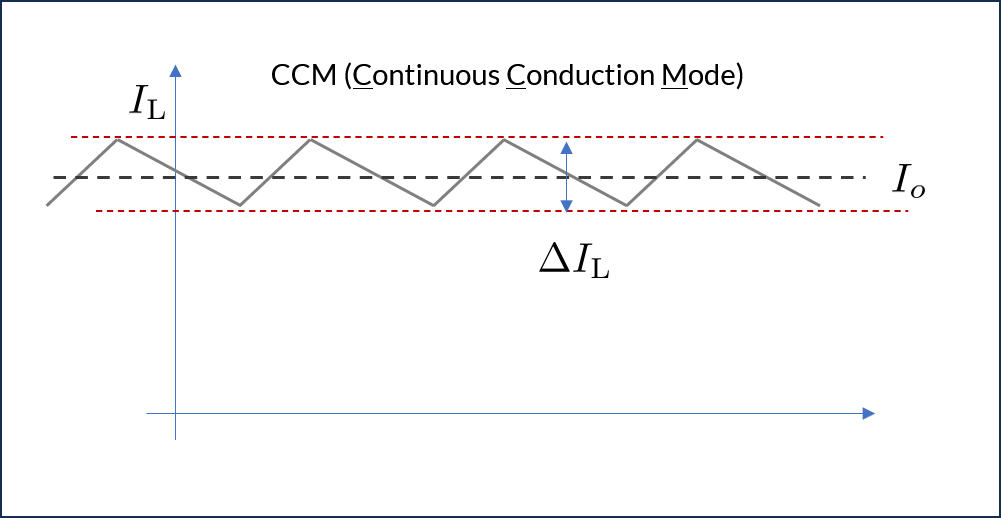
スイッチがonの時の電圧の関係は以下の式になる($I_\mathrm{L}$の向きを負荷に流れる向きにする):
\[ V_i = L\cfrac{dI_\mathrm{L}}{dt} + V_o. \]onの時の時間($T_s \times D$)だけに限定すると上の式は次のようになる:
\[ V_i = L\cfrac{\Delta I_\mathrm{L}}{D T_s} + V_o. \]ここで、$I_\mathrm{L}$の増減量 $\Delta I_\mathrm{L}$を使った。
さらに$I_o$を出力電流の平均値として、$r \triangleq \Delta I_\mathrm{L} /I_o$ (CRは時定数と紛らしいので避けた)とすれば
\[ V_i = L\cfrac{r I_o}{D T_s} + V_o. \]と書ける。
\[ V_o = D V_i \]を使うと
\[ \cfrac{V_o}{D} = L\cfrac{r I_o}{D T_s} + V_o. \]これを$L$を左辺にして整理すれば簡単に
\[ L = \cfrac{(1-D) V_o T_s}{r I_o} . \]とめでたくANALOG DEVICESのページの式に辿りつく。
r の大きさはANALOG DEVICESによれば「0.3がよく使われる」とある。 TEXAS INSTRUMENTSのアプリケーション・ノートでは、「0.25-0.5」とある。
シミュレーション
上記の$r$でどのようにbuck converterが振る舞うかをシミュレーションしてみよう。
下図のようなSimscapeモデルでやってみた。簡単のため負荷は抵抗にしている。
パラメーターは以下の通り:
Vi = 24; % [V] input voltage
D = 0.4; % duty ratio
f_s = 100e3; % [Hz] switching frequency
t_s = 1 / f_s; % [sec] switching period
Co = 100e-6; % [F] output Capacitor
Ro = 1; % [ohm] output resistor
なおPWMを使うスイッチング回路のシミュレーションではソルバーの時間ステップをスイッチング周期の2桁程度小さい値、あるいは必要に応じてそれ以下にする。 PSIMでは1周期を50ポイント分割するのが目安と言っている(How to Select a Timestep in PSIM)。 スイッチング周期よりも十分小さい時間ステップにしていないとPWM波形を適切に扱えない。 可変ステップの場合は最大ステップサイズをスイッチング周期のおよそ2桁下の値を入れれば良い。
上のパラメーターの場合、スイッチング周期が10$~\mu$sec = 1e-5 secなので、最大ステップを1e-7にしている。
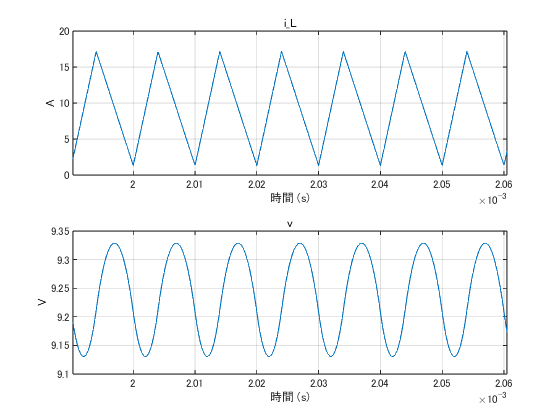
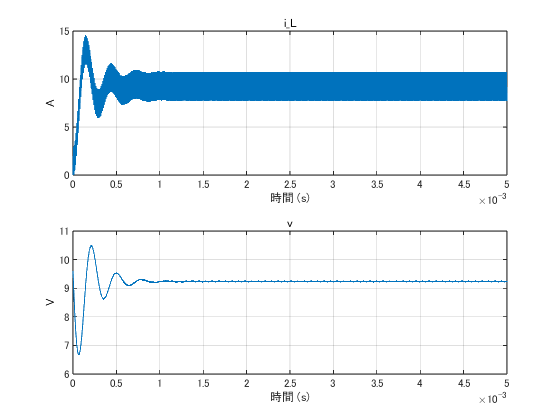
$r = 0.3$の場合
これがANALOG DEVICESでは一般的という値。 この場合は$L = 20~\mu$Hになる。
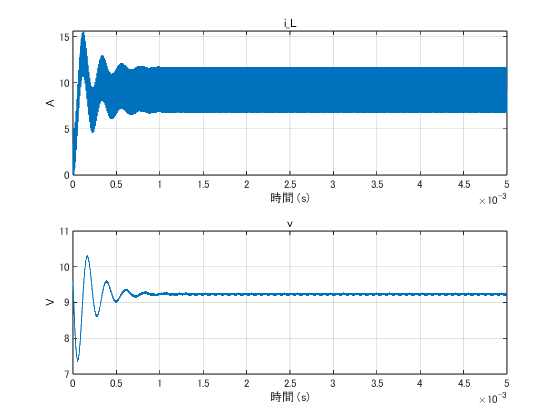
$r = 0.5$の場合
この場合は$L = 12~\mu$Hになる。
$r = 0.2$の場合
この場合は$L = 30~\mu$Hになる。
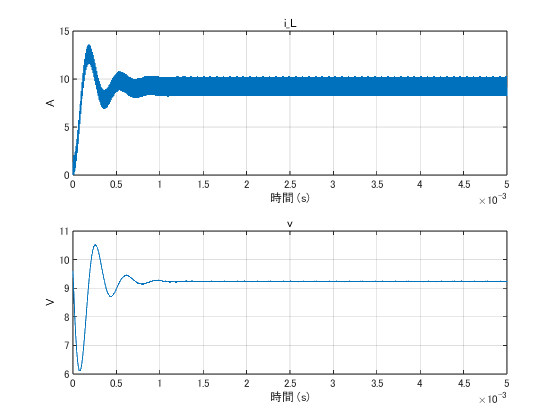
$r = 1.6$の場合
TEXAS INSTRUMENTSのアプリケーション・ノートに書いてあるが、$r = 2$は理論上の連続電流モード(CCM)と電流不連続モード(DCM)の境目で、$r=1.6$はぎりぎりCCMの場合に相当する。 この場合、設計値は$L = 3.8~\mu$Hになる。
スイッチやダイオードでの電圧降下があるため、出力電圧がデューティー比×入力電圧値よりも若干下がる。 上の式で$r=2$を代入して得られる$L$ではDCMになってしまう。 TEXAS INSTRUMENTSのアプリケーション・ノートに書いてあるように、スイッチやダイオードでの電圧降下を考慮した式を使うほうが良さそうだが、自分は試していない。
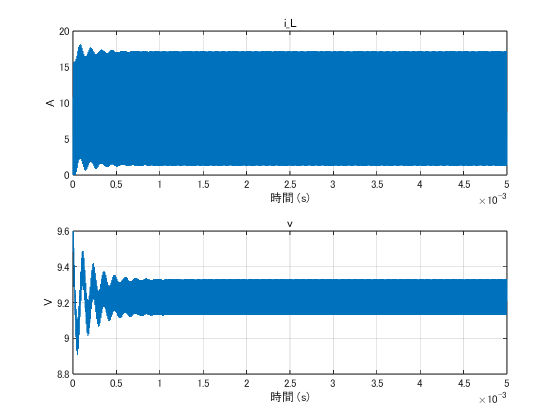
時間軸を拡大すると下のようになる。ほとんどDCMになりそうな状態だ。