ランダウ・リフシッツ力学 §32 問題3

ランダウ・リフシッツの力学(増補第3版) §32 問題3のメモです。

物理振り子(実体振り子)の様子を下のように考えます:

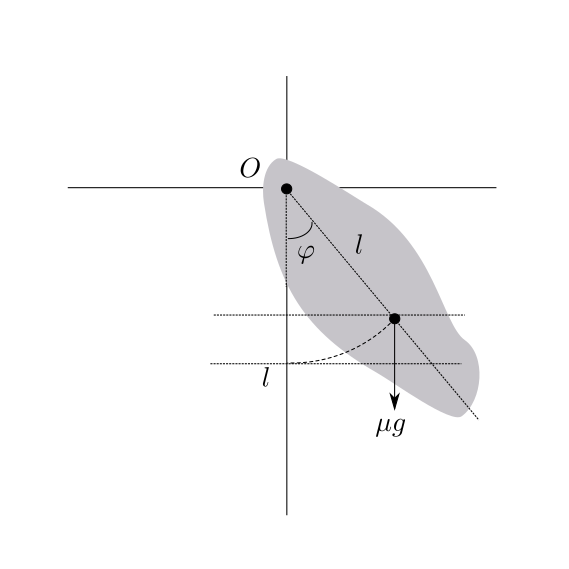
ポテンシャル・エネルギーは

\begin{align} U & = \mu g l (1 – \cos \varphi) \\ &= \mu g l \cfrac{\varphi^2}{2} \end{align}

回転軸を図中の\(O\)として、各慣性主軸との角度をそれぞれ\(\alpha\), \(\beta\), \(\gamma\)とすると、角速度の各慣性主軸への投影は\(\dot{\varphi} \cos \alpha\), \(\dot{\varphi} \cos \beta\) \(\dot{\varphi} \cos \gamma\)になります。

ラグランジアン\(L\)は

\begin{align} L & = \cfrac{1}{2} \mu \dot{\varphi}^2 + \cfrac{1}{2}\left[ I_1 \dot{\varphi}^2 \cos^2 \alpha + I_2 \dot{\varphi}^2 \cos^2 \beta + I_3 \dot{\varphi}^2 \cos^2 \gamma \right ] – \mu g l \cfrac{\varphi^2}{2} \\ & = \cfrac{1}{2} \dot{\varphi}^2 \left[ \mu + I_1 \cos^2 \alpha + I_2 \cos^2 \beta + I_3 \cos^2 \gamma \right ] – \mu g l \cfrac{\varphi^2}{2} \end{align}

運動方程式を立てると

\begin{align} \cfrac{d}{dt} \cfrac{\partial L}{\partial \dot{\varphi}} – \cfrac{\partial L}{\partial \varphi} = & 0 \\ \left[ \mu + I_1 \cos^2 \alpha + I_2 \cos^2 \beta + I_3 \cos^2 \gamma \right ] \ddot{\varphi} + \mu g l \varphi = & 0 \\ \ddot{\varphi} + \cfrac{\mu g l}{\left[ \mu + I_1 \cos^2 \alpha + I_2 \cos^2 \beta + I_3 \cos^2 \gamma \right ]} \varphi = & 0 . \end{align}

これから

\[ \omega^2 = \cfrac{\mu g l}{ \mu + I_1 \cos^2 \alpha + I_2 \cos^2 \beta + I_3 \cos^2 \gamma } . \]